What is the meaning of RMS?

luzhaoxin_2004 · September 18, 2006, 3:14pm

I know it is root mean square.
For example a,b,c,d,e,f
RMS=sqrt((aa+bb+cc+dd+ee+ff)/6)
Is it right?

moneta · September 18, 2006, 4:19pm

If you mean the RMS defined in an histogram, it is the standard deviation,
not the root mean square,

see root.cern.ch/root/html/TH1.html#TH1:GetRMS

luzhaoxin_2004 · September 19, 2006, 2:39pm

[quote=“moneta”]If you mean the RMS defined in an histogram, it is the standard deviation,
not the root mean square,

see root.cern.ch/root/html/TH1.html#TH1:GetRMS[/quote]
I find RMS in Users_Guide_5_12.pdf
see root.cern.ch/root/doc/RootDoc.html
page 57.Statistics Display:
the root mean square (RMS)
IS it right?

luzhaoxin_2004 · September 19, 2006, 3:14pm

could you tell me all the meaning of “the 7 statistic display” in my plot?
thanks!
i fit the histogramm with gaus

moneta · September 19, 2006, 4:49pm

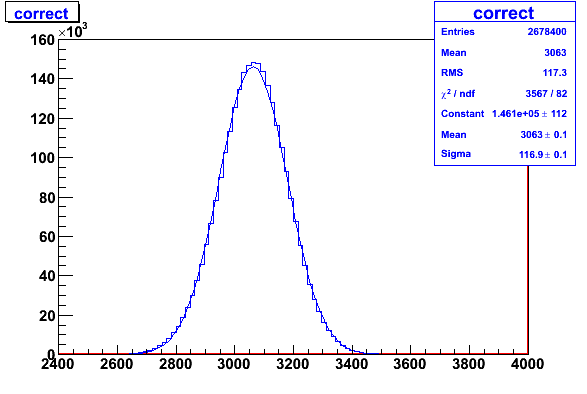
As I said before, the meaning of RMS is standard deviation. This is common in physics, as it is mentioned also in

mathworld.wolfram.com/Root-Mean-Square.html

I agree, we should indicate that clearly also in the User guide.

Concerning the picture:

Mean: Average of the histogram entries
RMS: Standard deviation of the histogram entries
Chi2: Chi2 value obtained from the fit :
Sum squares of the normalized residuals :

           Sum [( bin content - function value)/binError]^2

ndf : number of degree of freedom in the fit =
number of bins used in calculating the chi2 - number of fit parameters

then we have the fitted parameters :

Constant: is the amplitude of the fitted Gaussian function
Mean : is the mean of the gaussian
sigma: standard deviation of the gaussian

In case of perfect gaussian data and infinite statistics RMS -> sigma

I hope it is clear,

Regards,

Lorenzo

luzhaoxin_2004 · September 20, 2006, 12:23am

[quote=“moneta”]As I said before, the meaning of RMS is standard deviation. This is common in physics, as it is mentioned also in