Univariate and Multivariate Gaussian Distributions

[spyhunter01]

Hi all,

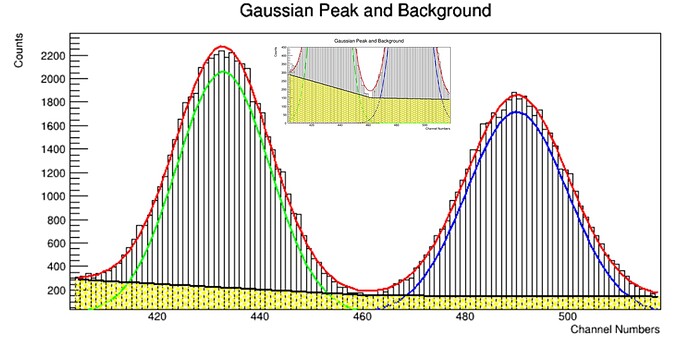
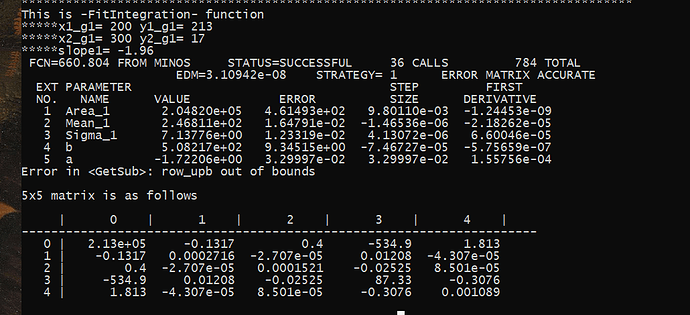
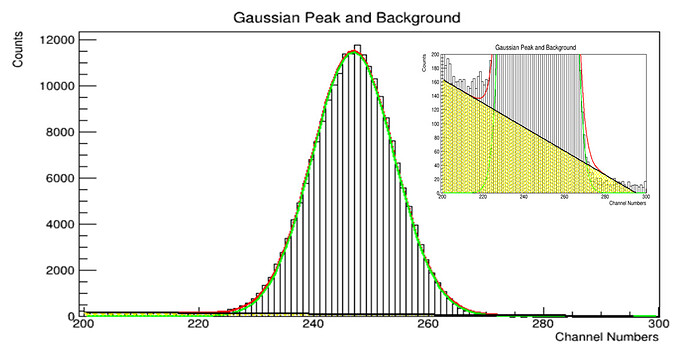
Let’s imagine we focus on a single 661keV Cs-137 peak in the first case.
Then, in the next case, we focus on 2 overlapping peaks like 1173keV and 1332keV from a Co-60 source. In both situation, please consider only the 3 to 4 sigma peak coverage, so we are not interested in the entire spectra we collected. As you all know, the data from a detector can be extracted on a text file as 1 columb showing the counts corresponding each channel. Thus, you now get a discrete data. When you fit Gaussian function on those peaks, you have continuous data representation.

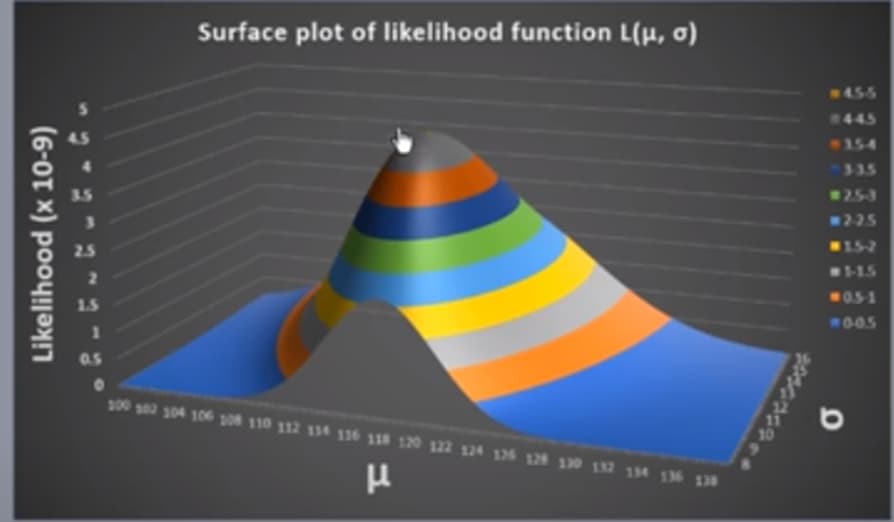
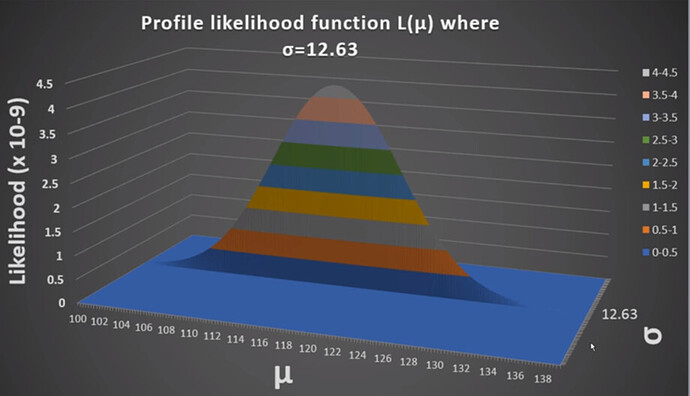
I think the counts as a vector, or random variable of the PDF fuction for Normal distribution. Depending on the peak number, you have either one mean and sigma like in Cs-137 case, or two means and sigma like in Co-60 case.

Question 1:
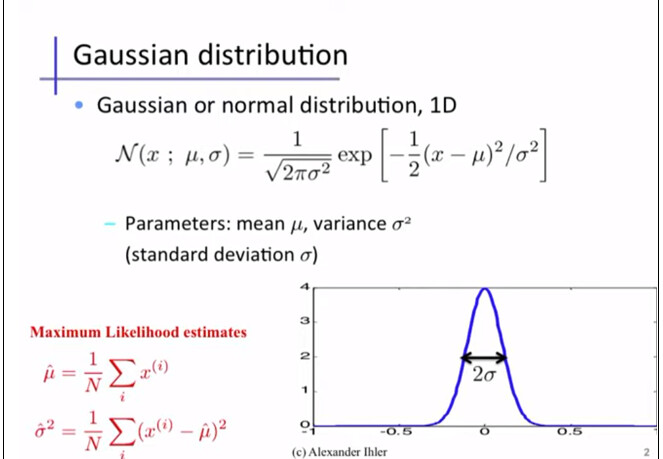
Now, will you consider Cs-137 case as a univariate Gaussian distribution case with random scalar variables contructed by the counts?
Question 2:
If you said yes to question one, then can we say we don’t need matrix notations for calculations? Can we also say that we don’t need covariance matrix for Sigma because there is onle one parameter for the mean and sigma?
Question 3:
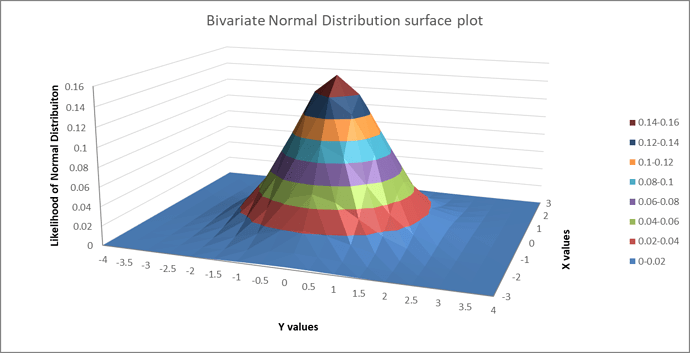
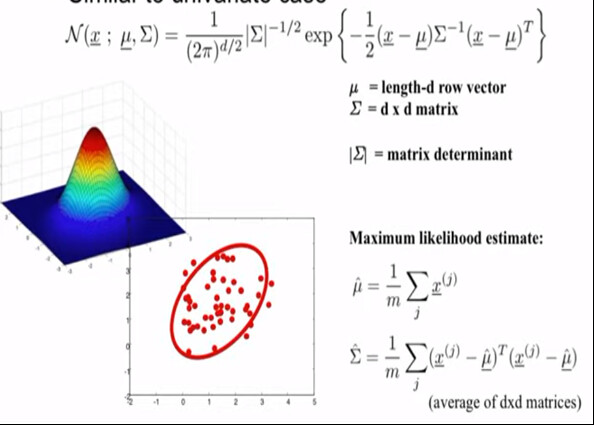
Will you consider Co-60 case as a multivariate Gaussian distribution case (in specific you can call it bivariate case) with random scalar variables contructed by the counts? That’s because we have a data set of counts, we have two means and two sigmas in total to fit, so we need matrix and vector notations in our calculations.

Some pictures to help to visualize the questions:

Cheers.

[jonas]

Hi @spyhunter01, thanks for the question!

Question 1:
Now, will you consider Cs-137 case as a univariate Gaussian distribution case with random scalar variables contructed by the counts?

Yes, and if you add the Co-60 peak, the distribution is the normalized sum of two Gaussians.

Question 2:
If you said yes to question one, then can we say we don’t need matrix notations for calculations? Can we also say that we don’t need covariance matrix for Sigma because there is onle one parameter for the mean and sigma?

The question is not relevant I think, because it’s not a multivariate Gaussian.

Question 3:
Will you consider Co-60 case as a multivariate Gaussian distribution case (in specific you can call it bivariate case) with random scalar variables contructed by the counts? That’s because we have a data set of counts, we have two means and two sigmas in total to fit, so we need matrix and vector notations in our calculations.

No, I would for sure not consider it as a multivariate Gaussian distribution, because there is only one variable: your detector response. It’s a univariate problem. Your distribution is the sum of Gaussians, not the product.

Meaning that if you treat your situation with a multivariate Gaussian, you will get the wrong results, because an uncorrelated multivariate Gaussian is the product of the univariate components. In your situation however, you need to add Gaussians and not multiply them.

If you want to fit the sum of different Gaussians in ROOT, you can look at this tutorial to get an idea on how to do it:
https://root.cern/doc/master/FittingDemo_8C.html

For more complicated fits, you can also take a look at RooFit.

Hope this helps!
Jonas

[spyhunter01]

@jonas

Yes, and if you add the Co-60 peak, the distribution is the normalized sum of two Gaussians.

I agree.

@jonas

The question is not relevant I think, because it’s not a multivariate Gaussian.

I agree since we said both Cesium-137 with one peak and Cobalt-60 with 2 peaks were univariate as can be seen from their 1D plots . I attach down v-below.
https://root-forum.cern.ch/

However, the reason why I asked why we use matrix notation and covariance matrix calcculations is because the integralerror (…) function in histogram root fitting has an input parameter of covariance matrix. Thus, you have to find it and give as an input to that function tp work.
Sample line of the function for your reference from my code:

double Gross_Area_g1 = total->Integral( g1_X_LBE, g1_X_UBE) / BinWidth ;
double Error_gross_g1 = total->IntegralError(g1_X_LBE, g1_X_UBE , p_total, cov_total.GetMatrixArray(),1e-5) / BinWidth;

For me, I have just counts corresponding each 1024 channels from my NaI(Tl) detector. That’s it, and I plot and analyze it. It has to be univariate casefor every peak seperately.

@jonas

No, I would for sure not consider it as a multivariate Gaussian distribution, because there is only one variable: your detector response. It’s a univariate problem. Your distribution is the sum of Gaussians, not the product.

I agree. I think you mean we only fit the total function on a data set, and this total function has Gaussian + polynomial background in it for 1 peak case as an illustration.

@jonas

because there is only one variable: your detector response.

I agree that our detector response as counts or signal or data set is our only scalar vector variable while we have only 2 fixed parameters, sigma and mean, for 1 Gaussian peak indeed. Well, you can make it 3 parameters if you wish by considering area or height as a seperate parameter in the case of Gaussian or normalized Gaussian cases.

All in all, I know how to fit things, but that covariance matrix in integraerror(…) function confused me. Do you have enough knowledge to clarify me on this.
Ref: https://root.cern.ch/doc/master/classTF1.html

@jonas

No, I would for sure not consider it as a multivariate Gaussian distribution, because there is only one variable: your detector response. It’s a univariate problem. Your distribution is the sum of Gaussians, not the product.

Meaning that if you treat your situation with a multivariate Gaussian, you will get the wrong results, because an uncorrelated multivariate Gaussian is the product of the univariate components. In your situation however, you need to add Gaussians and not multiply them.

I see now your point here.

One last question to my first plots in the first message, in what kind of situation in gamma-spectroscopy or in nuclear physics, we may have bivariate or multivariate gaussian distribution with more than one mean and sigma in the form of 2D, 3D, or more dimension plots? It’s because there is always 1D gaussian plots in gamma spectroscopy as far as I have come across so far.

[jonas]

Ah, I see now where you’re coming from with the IntegralError() function!

As explained in IntegralError() documentation, the covariance matrix there is the covariance matrix of the parameter estimation (i.e., the parameter uncertainties and their correlations). This is not the same as the covariance matrix that you’d use to specify your multivariate Gaussian as a model.

No matter what your fitting function is, you will get the final parameter covariance matrix in the ROOT fit result. I assume if your peaks are overlapping, you will also get non-zero diagonal elements for the sum of Gaussians and a background.

And indeed you have to pass this covariance matrix to IntegralError(), otherwise the the error propagation will not be done correctly:

TFitResultPtr r = histo->Fit(func, "S");
func->IntegralError(x1,x2,r->GetParams(),
                    r->GetCovarianceMatrix()->GetMatrixArray());

As for your last question about multivariate Gaussians in gamma spectroscopy: I can’t think of any example, but I’m also not that familiar with gamma spectroscopy (I’m more familiar with LHC physics).

[spyhunter01]

Yes, yes, you are all correct.

@jonas

As explained in IntegralError() documentation, the covariance matrix there is the covariance matrix of the parameter estimation (i.e., the parameter uncertainties and their correlations). This is not the same as the covariance matrix that you’d use to specify your multivariate Gaussian as a model.

I haven’t known that part, or I should say I wasn’t aware. I thought there was only one covariance matrix and it is in the multivariance case, not for the univariate 1D case.

Interestingly, in the one peak case of cesium, my output of covariance matrix didn’t give zeros for the off-diagonal part. I attach the output here down below.
I’d like you to explain me more about the covariance matrix of parameter estimation in 1D univariate case like in my pictures. Why or how we got a matrix for one gaussian peak since there is only one mean and sigma.

Output of 1 peak case in Cs-137:

In here, my total function I fitted on my data is 1 gaussian + 1 polynomial function. ThatS the output of the matrix where off diagonal part is nonzero. Not sure about the error in roe_upbound limit.

[jonas]

In a maximum likelihood fit, this covariance matrix is usually approximated by the second derivative of the likelihood function at the maximum (Hessian matrix). You can read more about it in various “statistical methods for particle physics” lecture slides, or in section 3.10 of this summary paper:

Practical Statistics for Particle Physicists

The diagonal elements are the best-fit parameter uncertainties squared. The off diagonal elements tell you how the best-fit value of one parameter depends on another parameter, in other words how much they are correlated in your fit model. Usually, none of the off-diagonal terms are zero, because the best-fit value of one parameter usually depends slightly on the other parameters. For example, if you vary the Mean_1 parameter a little bit in the model away from the best-fit value, your estimate for Sigma_1 would change because the data points are now further away from the mean. That’s what is meant with the covariance matrix of the parameter estimation.

This is something completely different from the covariance matrix you talked about in the multivariate Gaussian case, which would specify the correlation of observables, and not parameters.

I hope I understood you question correctly now, if not let me know!

[spyhunter01]

@jonas

This is something completely different from the covariance matrix you talked about in the multivariate Gaussian case, which would specify the correlation of observables, and not parameters.

Except that part, the rest I have already known , and I agree with you. I read that papers. Why you said observales not parameters for the multivariate case. Indeed, there is normally, x variable as a column vector in size d from your data set, and mu vector with same size as x, then dxd symmetric covariance matrix of Sigma just showing the sigma values correlation among each other, nothing else as a matrix in the calculations.

Anyways, I assume my question from your answer is answered. This matrix is just to show relation among parameters in the total functions that you fitted on your data. Nothing more. I wonder if I fit only gaussian on a data where there are only 3 parameters, how my 3x3 covariance matrix will be constructed for the uniavriate case. Will it be like this below, but with 3 parameters multiplications for each element in the matrix. Let’s say, height, mean and sigma.

For instance, there is no matrix in this calculation they claiim for a univariate case:

I assuma random variable x here represents our data, namely the counts here. However, matrix and vector notations come to play for multivariate case only like below as far as I researched so far.

I think that’s also a useful information for me about univariate case:

[Wile_E_Coyote]

In your “multivariate normal distribution” screenshot, the “#mu” vector has “d” independent components, and the “#Sigma” (symmetric) “d x d” covariance matrix has “d*(d+1)/2” independent elements. Thus, the “N” function has in total “d + d*(d+1)/2 = d*(d+3)/2” independent parameters.
So, when you fit this “N” function to some data, you will get the best fit values of “d*(d+3)/2” parameters, plus their (symmetric) “d*(d+3)/2 x d*(d+3)/2” covariance matrix with “d*(d+1)*(d+2)*(d+3)/8” independent elements (NOT to be confused with the “#Sigma” in the “N” function).

[spyhunter01]

Thanks, I stopped worry about multivariate case any more. I focused on univariate case where we always get with any gamma-ray detectors as counts in the form of Gaussian peaks.

My very first question was why we need a covariance matrix for 1D Gaussian distribution + pol background. I think I got my answer. It’s to show the correlations between gaussian paramaters and pol parameters, and then to use it in integral calculation in IntegralError(…) function I quoted earlier.

I was wondering for 1D univariate case, how we construct the cov-matrix with gauss+ 1st order or 2nd order pol paramaters. For instance, if we get 1st order pol background, we get in total 3+2 parameters comng from gauss and pol (height, mean, sigma, a, b). In this 5x5 matrix, first 3x3 sub matrix is for Gaussian and the another 2x2 matrix is for pol sub matrix correlations. I’d like to know how you write it in a matrix form. Can you take a photo after you write on a piece of paper the way how this matrix will look like if you don’t mind? (Or, screen shot from somewhere)

Sincerely Yours.

[Wile_E_Coyote]

As already written:

@jonas

In a maximum likelihood fit, this covariance matrix is usually approximated by the second derivative of the likelihood function at the maximum (Hessian matrix).

In a “chi2” fit, the covariance matrix is approximated by the second-order partial derivatives of the “chi2” function at the minimum.

[spyhunter01]

I keep checking Hessian matrix, not done yet. However, I had the calculation of parameter estimations from a website, he uses 1st order derivation of a gaussian. Well, there is hunders of nice videos, and most of them even are Prof. Dr. . Anyways, I wanna know how I apply to my situation, so I am still reading.

Ref: https://www.youtube.com/watch?v=Dn6b9fCIUpM&t=151s&ab_channel=StatQuestwithJoshStarmer

Cheers.

[spyhunter01]

@Wile_E_Coyote

In a “chi2” fit, the covariance matrix is approximated by the second-order partial derivatives of the “chi2” function at the minimum.

I am using likelihood method, so it should be the first derivative.
Ref: https://www.youtube.com/watch?v=Dn6b9fCIUpM&ab_channel=StatQuestwithJoshStarmer

[spyhunter01]

Anyways,

can you guys by any chance know why I am having this code error (Error in <operator=(const TMatrixT &)>: matrices not compatible) ! The code also doesn’t seem showing me polynomial submatrix at all for some reason. I use Print() function of it . It gives mt total matrix and submatrix for gaussian.

I attach the data and the code.
TestMatrix1.cpp (5.1 KB)
CS137.txt (10.0 KB)

The relevant part I am asking in the code:

cov_total.Print();
cov_g1.Print();
cov_bcg.Print();

Thanks a lot in advance.

[Wile_E_Coyote]

cov_bcg.ResizeTo(2, 2); cov_bcg = cov_total.GetSub(3, 4, 3, 4); // pol1
cov_bcg.ResizeTo(3, 3); cov_bcg = cov_total.GetSub(3, 5, 3, 5); // pol2

[spyhunter01]

Interesting, it shows the pol sub-matrix now, but the error of “Error in <operator=(const TMatrixT &)>: matrices not compatible” remains. What’s this error about?

[spyhunter01]

Guys, please tell me you actuall do not create this ugly looking formula by using cofactor and minor matrices methods to create covariance matrix when we sum Gaussian and polynomial function to fit on our data.

Ref: this is just the simple interpolation technique with matrices to find the fit parameters for a polynomial fit only. I guess I can extend to any function at all. This example for quadratic form of polynomial function.

Does cov-matrix look like this?

Or, you use finite difference method to find the square cov-matrix?

[moneta]

Hi,
The matrix formulation you show above (with the Z matrix) can be used in case of a linear fit, where the direct solution of the fit using matrix equation can be found. This is teh case when fitting for example a polynomial function.
In the case of a Gaussian fit, it is not anymore linear and you need an algorithm to find numerically the minimum of your likelihood (or least-square) function.
A gradient based method like Minuit uses the derivatives of the likelihood (or least-square) with respect to the parameters, which are computed by numerical differences. It is however possible to use also analytical derivatives or computed using automatic differentiation.
The ROOT TFormula class allows to compute those.
The covariance matrix is also computed in the same inverting the Hessian matrix, second derivatives of the likelihood (or least-square) function.

Lorenzo