Trouble Understanding Minuit2 Output

[christianwos83]

Hi all,

I am running the following chisquared minimization in Minuit2. I know that as it is, Minuit does not converge, but my question is more about how Minuit explores the values of parameters during the process.

Here is my code:

#include "Minuit2/FunctionMinimum.h"
#include "Minuit2/MnUserParameters.h"
#include "Minuit2/MnUserParameterState.h"
#include "Minuit2/MnPrint.h"
#include "Minuit2/MnMigrad.h"
#include "Minuit2/MnMinos.h"
#include "Minuit2/MnPlot.h"
#include "Minuit2/MnContours.h"
#include "Minuit2/FCNBase.h"
#include <utility> //std::pair
#include <iostream>
#include <iomanip>
#include <string>
#include <vector>
#include <cmath>
#include <Eigen/Dense>

using namespace ROOT::Minuit2;
using namespace Eigen;

const double PI = 4*atan(1);
// Define minimizer class (inherits from FCNBase)
class Minimizer : public FCNBase {

private:

  const std::vector< std::vector<double> > &m_data;
  //  const std::vector<double> &m_mass;

public:

  Minimizer(const std::vector< std::vector<double> > &data) : m_data(data) {}

  ~Minimizer() {}
  // functions to find factorial and double factorial of given number - used in th\
e Vqq matrix element
  unsigned int doublefactorial(unsigned int number) const
  {
    if (number == 0 || number == 1)
      return 1;
    return number*doublefactorial(number-2);
  }

  unsigned int powerfactorial(unsigned int number) const
  {
    if (number == 0)
      return 2;
    return pow(2,number + 1)*powerfactorial(number-1);
  }

  double diagonalization(double n, double L, double p0, double p1, double p2, double p3) const {
    // Declare the number of terms in the expansion and the number of iterations for the numerical integrals
    int N1 = 12;

    // Declare the variational parameters - values taken from the hybrid decay paper: https://arxiv.org/abs/2005.10850
    double alphaInit = 0.005;
    // Define the matrices - the dimension can be set to be any of the above indexes since they are generally the same
    MatrixXd HMX(N1, N1);
    MatrixXd NMX(N1, N1);
    MatrixXd KMX(N1, N1);
    MatrixXd VMX(N1, N1);

    //Declare the variables for the minimum eigenvalue
    double minEvalue0 = 0.0; // ground state eigenvalue
    double minEvalue1 = 0.0; // first excited state eigenvalue
    double minEvalue2 = 0.0; // second excited state eigenvalue
    double minEvalue3 = 0.0; // third excited state eigenvalue

    std::vector<double> eValues0;
    std::vector<double> eValues1;
    std::vector<double> eValues2;
    std::vector<double> eValues3;
    std::vector<double> minEvalues;

    // Loop over the variational parameters and the matrix elements (k1=n', l1=m', k2=n, l2=m).
    for (double alpha = alphaInit; alpha <= 1.000; alpha += 0.005){
      for (int k1 = 1; k1 <= N1; k1++){
        for (int k2 = 1; k2 <= N1; k2++){
          // Define the full Hamiltonian in configuration space - works for all values of L
          // Overlap Matrix
          NMX(k1-1,k2-1) = pow(2.0,L + 1)*sqrt(2.0)*pow(k1*k2,0.75 + L/2.0)/(pow(k1+k2,1.5 + L));
          // Mass and kinetic terms
          KMX(k1-1,k2-1) = (pow(2.0,L + 1)*sqrt(2.0)*pow(k1*k2,0.75 + L/2.0)/(pow(k1+k2,1.5 + L))) * (2.0*p0 + (3.0+2.0*L)*(k1*k2)*alpha*alpha/(p0*(k1+k2)));
          // Potential term
          VMX(k1-1,k2-1) = (powerfactorial(L)*pow(k1*k2,0.75 + L/2.0)/(doublefactorial(2*L+1)*sqrt(PI)*alpha*pow(k1+k2,2.0+L)))*(2*p1*alpha*alpha*(k1+k2)-3*(L+1)*p2);
        }
      }
      // Diagonalize and print the eigenvalues
      HMX = KMX - (4.0/3.0)*VMX;

      std::setprecision(8);
      GeneralizedSelfAdjointEigenSolver<MatrixXd> es(HMX,NMX);
      //pushback eigenvalues into vectors
      eValues0.push_back(es.eigenvalues()[0]);
      eValues1.push_back(es.eigenvalues()[1]);
      eValues2.push_back(es.eigenvalues()[2]);
      eValues3.push_back(es.eigenvalues()[3]);

    }
    // Calculate the minimum eigenvalue and the corresponding parameters
    minEvalue0 = eValues0[0];
    minEvalue1 = eValues1[0];
    minEvalue2 = eValues2[0];
    minEvalue3 = eValues3[0];
    //cout << "\n";
    //cout << "Here is the full list of eigenvalues: " << std::endl;

    for(unsigned int i = 0; i < eValues0.size(); i++){
      if (eValues0[i] < minEvalue0){
        minEvalue0 = eValues0[i];
      }
    }
    for(unsigned int i = 0; i < eValues1.size(); i++){
      if (eValues1[i] < minEvalue1){
        minEvalue1 = eValues1[i];
      }
    }

    for(unsigned int i = 0; i < eValues2.size(); i++){
      if (eValues2[i] < minEvalue2){
        minEvalue2 = eValues2[i];
      }
    }
    for(unsigned int i = 0; i < eValues3.size(); i++){
      if (eValues3[i] < minEvalue3){
        minEvalue3 = eValues3[i];
      }
    }
    //push_back all the minimized eigenvalues into a vector
    minEvalues.push_back(minEvalue0);
    minEvalues.push_back(minEvalue1);
    minEvalues.push_back(minEvalue2);
    minEvalues.push_back(minEvalue3);

    double eigenvalue = minEvalues[n-1]-p3;//return the desired eigenvalue from minEvalues
    return eigenvalue;
  }

    std::vector<std::string> particleNames ={"eta_b(1S)", "Y(1S)", "chi_b0(1P)", "chi_b1(1P)", "h_b(1P)", "chi_b2(1P)", "Y(2S)", "Y(1D)", "Y(2D)", "chi_b0(2P)", "chi_b1(2P)", "h_b(2P)", "chi_b2(2P)", "Y(3S)", "Y(4S)", "eta_2(2S)"};
    double operator() (const std::vector<double> &params) const {
      double X2 = 0.0;
      double relErr = 0.0;
      for (int i=0; i< m_data[0].size(); i++) {
        double n = m_data[0][i];
        double L = m_data[1][i];
        double f = diagonalization(n, L, params[0], params[1], params[2],params[3]);
        relErr = abs(m_data[2][i]-f)*100.0/m_data[2][i];
        X2 += (m_data[2][i] - f)*(m_data[2][i] - f);
        std::cout << "params: " << params[0] << ", " << params[1] << ", "
                  << params[2] << ", " << params[3] << std::endl;
        std::cout << std::setw(10) << particleNames[i] << ", exp[" << i << "] = " << std::setw(10) << m_data[2][i]
                  << " || theory[" << i << "] = " << std::setw(10) << f << " || relative error = " << relErr << " %" << std::endl;
      }
      std::cout << "\n";
      std::cout << "params: " << params[0] << ", " << params[1] << ", " << params[2] << ", " << params[3] << std::endl;
      std::cout << X2 << std::endl;
      return X2;
    }
    //set to 1 for chi-sq and 0.5 for log-likelihood
    double Up() const {return 1.0;}
  };

    int main(){

    std::vector< std::vector<double> > data(3);
    // bottomonium experimental states
    //eta (1S) n=1, L=0; N=0
    data[0].push_back(1.0);
    data[1].push_back(0.0);
    data[2].push_back(9.390);
    //Y (1S) n=1, L=0; N=0
    data[0].push_back(1.0);
    data[1].push_back(0.0);
    data[2].push_back(9.4603);
    //chi_b0 (1P) n=2, L=1; N=0
    data[0].push_back(1.0);
    data[1].push_back(1.0);
    data[2].push_back(9.8594);
    //chi_b1 (1P) n=2, L=1; N=0
    data[0].push_back(1.0);
    data[1].push_back(1.0);
    data[2].push_back(9.8928);
       //h_b (1P) n=2, L=1; N=0
    data[0].push_back(1.0);
    data[1].push_back(1.0);
    data[2].push_back(9.899);
    //chi_b2 (1P) n=2, L=1; N=0
    data[0].push_back(1.0);
    data[1].push_back(1.0);
    data[2].push_back(9.9122);
    //Y (2S) n=2, L=0; N=1
    data[0].push_back(2.0);
    data[1].push_back(0.0);
    data[2].push_back(10.0233);
    //Y (1D) n=3, L=2; N=0
    data[0].push_back(1.0);
    data[1].push_back(2.0);
    data[2].push_back(10.1611);
    //Y2 (1D) n=3, L=2; N=0
    data[0].push_back(1.0);
    data[1].push_back(2.0);
    data[2].push_back(10.1637);
    //chi_b0 (2P) n=3, L=1; N=1
    data[0].push_back(2.0);
    data[1].push_back(1.0);
    data[2].push_back(10.2325);
    //chi_b1 (2P) n=3, L=1; N=1
    data[0].push_back(2.0);
    data[1].push_back(1.0);
    data[2].push_back(10.2555);
    //h_b (2P) n=3, L=1; N=1
    data[0].push_back(2.0);
    data[1].push_back(1.0);
    data[2].push_back(10.2598);
    //chi_b2 (2P) n=3, L=1; N=1
    data[0].push_back(2.0);
    data[1].push_back(1.0);
    data[2].push_back(10.2686);
    //Y (3S) n=3, L=0; N=2
    data[0].push_back(3.0);
    data[1].push_back(0.0);
    data[2].push_back(10.3552);
//Y (4S) n=4, L=0; N=3
    data[0].push_back(4.0);
    data[1].push_back(0.0);
    data[2].push_back(10.580);
    //Y (2S) n=4, L=1, N=2
    data[0].push_back(2.0);
    data[1].push_back(0.0);
    data[2].push_back(9.999);

    //Create FCN function
    Minimizer fcn(data);

    //Create parameters
    double mq = 4.7;
    double alphaS = 0.34;
    double b = 0.19;
    double shift = 0.1;

    MnUserParameters uParams;//use params[i]/5 error
    uParams.Add("mq", mq, 0.2*mq);
    uParams.Add("alphaS", alphaS, 0.2*alphaS);
    uParams.Add("b", b, 0.2*b);
    uParams.Add("shift", shift, 0.2*shift);


    std::cout << "Computing the values of the parameters..." << std::endl;
    for (int i=0;i<data[0].size();i++) {
      std::cout << i << " "  << data[2][i]  << " : " << fcn.diagonalization(data[0][i],data[1][i],mq,alphaS,b) << std::endl;
    }
    //minimize
    //Minimizer fcn(data);

    //Set strategy to High
    MnStrategy strategy;
    strategy.SetHighStrategy();

    MnMigrad migrad(fcn, uParams);

    //fix a parameter
    //migrad.Fix("shift");

    FunctionMinimum min = migrad();

    std::cout << "\n";
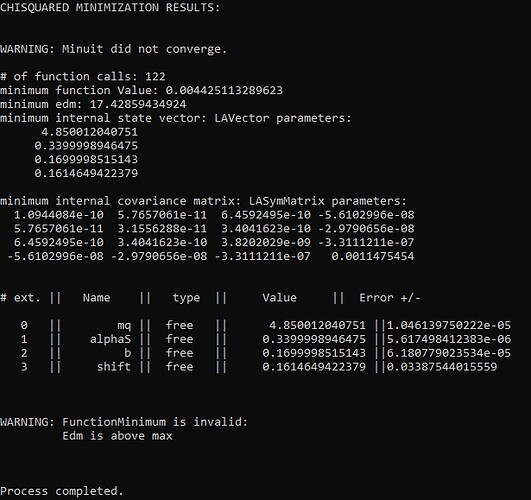
    std::cout << "CHISQUARED MINIMIZATION RESULTS:" << std::endl;
    std::cout << "\n";
    std::cout << min << std::endl;
    std::cout << "Process completed." << std::endl;

    return 0;
  }

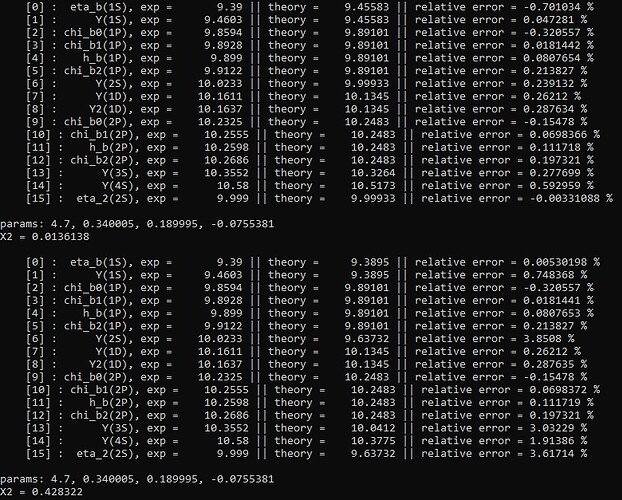
It is my understanding that in order to find the minimum for the objective function, Minuit2 will ‘explore’ various values of the parameters. But when I echo print the values of the parameters to the screen this is what I get.

So, the values of the parameters are the same in both runs, but the X2 value AND the theory masses produced by my code with those parameters are different???
Am I missing something in the way Minuit2 works? Any help would be greatly appreciated. Thanks.

Christian

ROOT Version: Minuit2 StandAlone version 6.15
Platform: Linux Mint 17
Compiler: gcc

[ynikitenko]

Hi Christian,

it looks like your output is not complete (it doesn’t print the final messages from your program).
However, I guess that parameters change somewhere during the run.
In your function there is an iteration on data. In MLE, for each data point the likelihood is calculated. The function to be minimized is the sum of these log likelihoods,

Maximum likelihood estimation

(this is a general idea, but I’m not sure whether MLE is implemented in your code or another objective function). Anyway, parameters in your code don’t change during the iteration on data. See the whole log to check whether they change (and the answer from Minuit).

In general, gradient descent traverses parameter space in the direction of the fastest decrease of the function. If you’ve more specific questions, feel free to ask further.

[christianwos83]

Dear ynikitenko,

Thank you for your reply. I did not post the entire output, what I posted was a screenshot that I took while the program was still running. The final output is the following.

I am implementing the chisquared objective function, not the MLE. You mentioned the log to check whether they change or not. Is the log what FunctionMinimum provides when I print the answer to the screen, or are you referring to something else?

Also, as I watch the entire process, the parameters do change, although only slightly, from one run to another in general, but I was confused as to why sometimes the program prints the same parameters while the value of the chisquared changes.

Thank you again,
Christian

[ynikitenko]

Could you please plot the data and the function?
I can see from the output that your parameters have very tiny errors. Probably this means that your fit is very sensitive to these parameters, that’s why they can’t be changed much during the minimization (they could be known very precisely, if the fit converged).

If you fit doesn’t converge, maybe the function does not describe the data well, and should be changed? Also, since Minuit finds the local minimum, you should try different initial values of parameters.
If your parameters change in the end, you don’t have to worry that they are constant during some intermediate steps.

Cheers,
Yaroslav

[christianwos83]

The function actually does not do a bad job at modeling the data, in my opinion.

But I am concerned as to why the minimization fails.

Thanks again.

[ynikitenko]

yes, that is strange. Why would it not converge? Did you try to set verbose option to Minuit? It should print some errors and warnings.
UPD: you can copy the output and add it as a text file here if you wish (maybe better than a screenshot, at least for a lot of text).

[ynikitenko]

I’m also a bit confused why you have only 4 parameters in the last output of fit results. In the beginning you had many more. If your function does not depend much on the parameters, the fit would not converge (it will have no minima). To have a minimum, in the parameter space of your function (chi2 sum) the function must be convex (like a parabola for each coordinate).
UPD: If you take a linear function, the minumum will be just at the border of the possible range of the parameters. Try to tune the ranges (is your function well defined for the whole range?..).

[christianwos83]

I have only four parameters in my model. I kept printing them over and over, after every single iteration, and at the end of each function call, to see if something fishy was happening.

And yes, my function is well-defined everywhere.

Thanks,
Christian

[ynikitenko]

I see.

I think convergence mostly depends on the function and parameters. You can take a linear function to test that your code works.

Me personally don’t always get answers from Minuit and I don’t know why yet. Try to simplify your model (or maybe add more details to that?..).

There are examples of working minimizations in $ROOTSYS/tutorials/roofit (RooFit is an excellent package for fitting).

I’m afraid I can’t help you any more with this, so I wish you good luck. Maybe someone else will answer.

Cheers,
Yaroslav

[christianwos83]

Thank you for all your help. I had already tested my code with a linear function and had achieved convergence. And thank you for suggesting looking into $ROOTSYS/tutorials/roofit. I will definitely check it out.

Best,
Christian

[ynikitenko]

Glad if that was useful. And one more idea. Minimization can fail because of numerical inaccuracies. Your parameters have very tiny errors, so that the floating precision may be too rough for them. Try to redefine them to avoid that.

Best,
Yaroslav