Tilt of ellipse in bigaus

[caforioroot]

Hello,

sorry for reopening this thread, I did not react quickly enough.
I have an ellipse-shaped distribution in a 2D histogram that I want to fit with the “bigaus” function.
The fit works very well, but I need the slope of the resulting function: is there a way to get this parameter?
The slope is the tangent to the angle alpha in the attached picture, so what I need is the angle corresponding to the tilt of the ellipse. Currently I am determining it by using the SigmaX and SigmaY:

“acos(sigma_x/sqrt(sigma_xsigma_x + sigma_ysigma_y))”

but the drawback is that since SigmaX and SigmaY are always positive I can only get angles < pi/2.

With thanks

Davide

ROOT version: 6.20/04
Ubuntu 20.04.3 LTS, Release: 20.04

[Wile_E_Coyote]

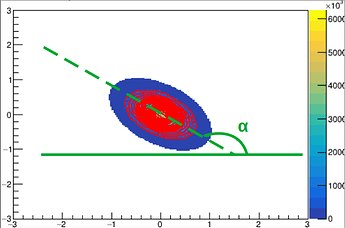
The “bigaus” is actually based on the “ROOT::Math::bigaussian_pdf” function (you can use the “rho”, “sigmax” and “sigmay” parameters to calculate the principal axes, which are defined by the eigenvectors of the covariance matrix, and the semidiameters, which are the square-roots of its eigenvalues):

{
  // ... create the function ...
  TF2 *f = new TF2("f", "[0] * ROOT::Math::bigaussian_pdf(x, y, [2], [4], [5], [1], [3])", -10., 10., -10., 10.);
  f->SetParNames("constant", "x0", "sigmax", "y0", "sigmay", "rho"); // note: -1 < rho < 1
  // f->Print();
  f->SetParameters(1000., 3., 2., 1., 3., -0.75); // "test" parameters' values
  // ... draw the function ...
  TCanvas *c = new TCanvas("c", "c");
  f->SetNpx(100); f->SetNpy(100);
  f->Draw("cont1z");
  gPad->SetGrid(1, 1);
  c->SetRealAspectRatio(1); // (1) or (2)
  // ... create the covariance matrix ...
  Double_t sigmax = f->GetParameter(2);
  Double_t sigmay = f->GetParameter(4);
  Double_t rho = f->GetParameter(5);
  TMatrixDSym covMatrix(2);
  covMatrix[0][0] = sigmax * sigmax; covMatrix[1][1] = sigmay * sigmay;
  covMatrix[0][1] = covMatrix[1][0] = rho * sigmax * sigmay;
  std::cout << "... covMatrix ..." << std::endl; covMatrix.Print();
  std::cout << "determinant = " << covMatrix.Determinant() << std::endl << std::endl;
  // ... calculate the principal axes ...
  TVectorD eigenValues;
  TMatrixD eigenVectors = covMatrix.EigenVectors(eigenValues);
  std::cout << "... eigenValues ..." << std::endl; eigenValues.Print();
  std::cout << "... eigenVectors ..." << std::endl; eigenVectors.Print();
  // ... draw the principal axes ...
  Double_t x0 = f->GetParameter(1);
  Double_t y0 = f->GetParameter(3);
  TArrow major(x0, y0,
               x0 + eigenVectors[0][0] * TMath::Sqrt(eigenValues[0]),
               y0 + eigenVectors[1][0] * TMath::Sqrt(eigenValues[0]),
               0.015, "|->");
  major.Draw();
  TArrow minor(x0, y0,
               x0 + eigenVectors[0][1] * TMath::Sqrt(eigenValues[1]),
               y0 + eigenVectors[1][1] * TMath::Sqrt(eigenValues[1]),
               0.015, "|->");
  minor.Draw();
}

For detailed description see:
Wikipedia → Multivariate normal distribution
Wolfram Mathworld → Bivariate Normal Distribution

[caforioroot]

Ok, thanks, that works fine!
I just wonder if there is a method/function to extract the eigenvectors from the covariance matrix: I did it myself and is just a few more lines in my code but if I could do that in one line it would be great.

Cheers

D.

[Wile_E_Coyote]

Well, I needed only a few more lines … see my previous post.