The deviation for the area under the Gaussian function and the difference between the 2 areas for 2 overlapped Gaussians

[spyhunter01]

Hi everybody,
Could you remind me how we can cover entire %100 of the Gaussian area by using Integral(…,…) for the function we defined earlier? I guess, we can’t write -infinity to + infinity as an option.
For instance:

TF1*f1= new TF1("f1","gaus", -10,10);
f1->SetParameter(0,10);
f1->SetParameter(1,0);
f1->SetParameter(2,2);
f1->Draw();
f1->Integral(-6, 6);  

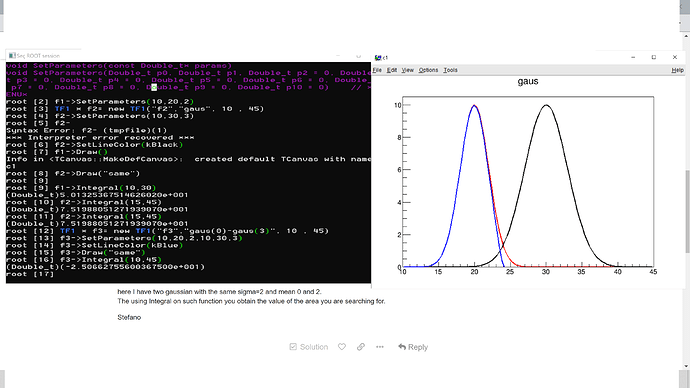
All we know, for example, we can cover 99.73% if we go range from -3sigma to +3sigma as I chose above from -6 to 6. Thus, I can retrieve the full area by dividing the result of this integral to 0.9973.

Also, the formulation says the area of a Gaussian is height x sigma x sqrt(2*pi) . When I compare the ROOT’s Integral result, they don’t match %100. For instance integral gives 50.128 after percentage correction, but formula gives 50.132.

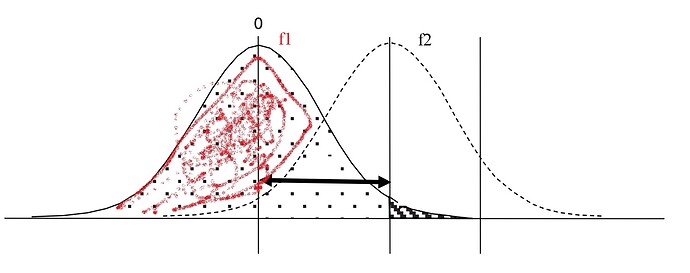
Another, more important question for me, is there any example to look at to get the blue area I badly marked in the picture I attached. It shows the simple case when 2 Gaussian functions are overlapped.
Mathematically, we can just get the integral of the (f1-f2) in the specified range on X axis. That will give immediately, the blue area. How should I implement that to my code, so ROOT understands? Probably, I will need errors, too. However, let’s get the 1st bit, first.

Appreciate to all in advance.

[Dilicus]

HI @spyhunter01,
when I compute the Integral in the range (-3sigma,3sigma) with the line below

@spyhunter01

f1->Integral(-6, 6)

I obtain 49.997218, that corrected is for the percentage 50.132576.

In any case to integrate gaussian I suggest you to integrate between -5sigma and 5 sigma, the result you obtain is already correct.

Regarding the second point of your question you can define a function as the difference of two gaussians

 TF1*f1= new TF1("f1","gaus(0)-gaus(3)", -15,15);

Then I set the parameters of both the gaussians with SetParameters.

f1->SetParameters(10,0,2,10,2,2)

here I have two gaussian with the same sigma=2 and mean 0 and 2.
The using Integral on such function you obtain the value of the area you are searching for.

Stefano

[spyhunter01]

First of all, thanks Stefano.

Is that correct that your line of " TF1*f1= new TF1(“f1”,“gaus(0)-gaus(3)”, -15,15); " actually represents the red area in my shape in ROOT coding. If so, that’s good news because how simple is that.

Why I got negative value on my screen for the simple example I did? I attached.

Code lines:

TF1 * f1= new TF1(“f1”,“gaus”, 10 , 45) ;
f1->SetParameters(10,20,2) ;
TF1 * f2= new TF1(“f2”,“gaus”, 10 , 45) ;
f2->SetParameters(10,30,3) ;
TF1 * f3= new TF1(“f3”,“gaus(0)-gaus(3)”, 10 , 45) ;
f3->SetParameters(10,20,2,10,30,3)
f1->Draw();
f2->Draw("same);
f3->Draw("same);
f3->Integral(10,45); // the answer is (Double_t)(-2.50662755600367500e+001)
if I say,
f3->Integral(10,24); //(Double_t)4.72812449233806120e+001
I calculated the intersection as 24. The graphs also shows 24. By coincidence, maybe this f3 ends around 24.
Is that because the max point that I gave to integral to calculate?

I think the range from -10 to 12 will be 5 sigma left from the 1st peak and 5 sigma right from the 2nd peak as you said instead of -15 to 15. However, I guess it won’t hurt anything at this stage, right? The main point will be to put the correct range when we write the integral part for this subtraction as f1->Integral(-10,12). Eventually, they go to infinity anyway, and that’s their common limits on both edges.

[dastudillo]

Draw f3 separately and see what it really looks like.

[Dilicus]

As dastudillo said the difference of the 2 gaussians is the one showed in the figure below

So a certain point you start to integrate negative value.

If instead you want to integrate just up to the intersection point you should do something like this

TF1*f2= new TF1("f2","gaus(0)>gaus(3)?gaus(0)-gaus(3):0", -10,10);
f2->SetParameters(10,0,2,10,2,2)
f2->Draw()

This is the difference of the two functions if the y of first gaussian is larger of the y of the second one, and is 0 otherwise.

This will give you the right answer.

Stefano

PS

Maybe try to use f2->SetNpx(200) just to have more points in the curve, the curve will look smoother

[spyhunter01]

I see. Of course, I haven’t set the Y values to show negative parts. Thus, I missed the point. Also, I haven’t set the integral limits narrower as you said. Therefore, I missed the possibility to have negative value after subtraction in terms of which integral has the most counts underneath it.

I guess I was tired. Thanks, man.

Now, I guess I start to work on the integral errors. Before I start, will that IntegralError(…) method work in this subtraction case as it was working only for 1 Gaussian case?

Cheers.

[Dilicus]

IntegralError should work fine