Hello Everyone,
I am working on the exponential decay fitting. After fitting I got the value of the constant [N_{0}], (guessed parameter).
The fitting equation is given here.
"[N_{0}]/[#tau].*exp(-x/[#tau])+[Constant]",
I am trying to know, how can I be sure that the N_{0} gives me the correct value of the initial particles?
Here is the plot of the decay.
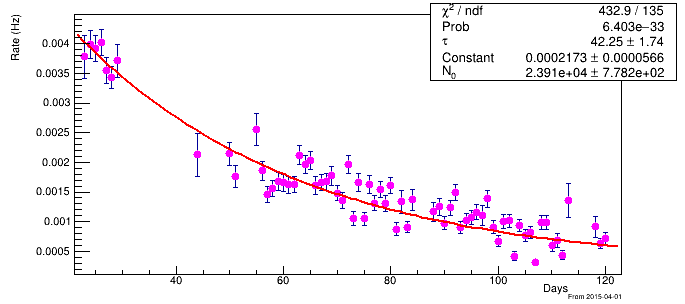
Thank you for your time.
Regards
Iftikhar
Please read tips for efficient and successful posting and posting code
ROOT Version: Not Provided
Platform: Not Provided
Compiler: Not Provided
Try to play with:
{
double xmin = 20., xmax = 125.;
int nx = int(xmax - xmin + 0.5);
int n = 1000;
gStyle->SetOptStat("e"); // "nemr"
gStyle->SetOptFit(1111);
TCanvas *c = new TCanvas("c", "c");
c->Divide(1, 2);
c->cd(1);
TF1 *f = new TF1("f",
"[N_{0}] / [#tau] * exp(-x / [#tau]) + [Constant]",
xmin, xmax);
f->SetParameter("N_{0}", 2.e4);
f->SetParameter("#tau", 40.);
f->SetParameter("Constant", 0.0002);
f->DrawCopy(); // uses the above parameters' settings
c->cd(2);
TH1D *h = new TH1D("h", ";Days;Rate (Hz)", nx, xmin, xmax);
if (!(h->GetSumw2N())) h->Sumw2(kTRUE);
h->FillRandom("f", n);
#if 0 /* 0 or 1 */
h->Scale(1. / n, "width");
// a better initial value
f->SetParameter("N_{0}", f->GetParameter("N_{0}") / TMath::Sq(xmax - xmin));
#else /* 0 or 1 */
// a better initial value
f->SetParameter("N_{0}", f->GetParameter("N_{0}") * n / (xmax - xmin) / nx);
#endif /* 0 or 1 */
h->Fit(f, "WL", "E");
c->cd(0);
}
1 Like
Hi Wile_E_Coyote,
Thank you for the code. Can you please provide some details of what you did after?
c->cd(2);
Does it find the appropriate parameters of [N_{0}] itself? I am not sure about it.
The other question I have is that, how do you know about this [N_0}] to be 2.e4? It’s a silly question but I want to know how can I guess this without plotting the fit?
f->SetParameter("N_{0}", 2.e4);
Thank you for your time. Appreciate
Regards
Iftikhar
I took the initial values from your plot in the first post here (well, they are “rounded” values, not the same). You can play with them as you like (i.e., you can set whatever values you like).
In the created “h” histogram, I try to simulate a decay spectrum according to the “f” function, which I then fit using this function (see the returned “best fit” values and compare them with the initial ones).
The descriptions of class methods that are used can be found in:
https://root.cern/doc/master/classTH1.html
https://root.cern/doc/master/classTF1.html
1 Like
Hello Wile,
Thank you for the prompt reply, I have a question about the initial parameters, Can you please tell me if there is any other way instead of guessing the initial parameter in this plot that I have?
(N_0 only because I already know the decay time already).
Also, can you please provide me a general idea of what did you wanted to get in the last few lines of your script?
Thank you very much.
Regards
Iftikhar
Knowing the “tau”, you can simply set the initial “Constant = 0;” (unless you know it’s approximate value in advance) and then set the initial “N_0” using the first bin of your “h” histogram, e.g. something like:
N_0 = (h->GetBinContent(1) - Constant) * tau * TMath::Exp(h->GetBinCenter(1) / tau);
1 Like
Hi Wile,
Thank you very much, I was exactly looking for this.
Simply knowing the y-axis, we can do something like this,
if we put t=0 in the function and then try to calculate, we can find the N_0.
N_0=( #tau) * the maximum value of y-axis of the data.
From the plot it can be done like this,
N_0= (42.25)(0.004)= 0.168.
That’s what I was thinking.
Thank you,
Regards
Iftikhar
