TF1 parameter error with TF1 function of C functions

ROOT
1

Dear Rooters,

I am trying to generate a TF1 function from others TF1 functions which are defined from a general C function.
When I run the simple following “test” example:

Double_t fun(Double_t *x, Double_t *p){
  return x[0]*p[0];
}

void test(){

  TF1 *f1 = new TF1("f1",fun,-4,8,1); 
  TF1 *f2 = new TF1("f2",fun,-4,8,1); 
  TF1 *f = new TF1("f","f1+f2",-4,8);  
 
}

I have these errors:

Error in <TFormula::Compile>: Empty String Error in <TF1::TF1>: function: f/f1+f2 has 0 parameters instead of 1

I have the impression that f1 and f2 are not understood in the formula, although
I can draw them, give them parameter values…

Am I understanding it right? And if so is there a way to work around this issue?

Best regards
Julien

2

Dear Rooters,

I did not solve directly my problem but I find a workaround using polynomial fits.
But somehow I bumped again in the same question of my first post: how to tell ROOT to “shift” the parameter number while adding previously defined user functions?
I first found that it works “by itself” while adding functions, although I do know that you are supposed to tell in your formula explicitly while using predefined formulas the parameter shift (ex: “gaus(0)+gaus(3)” instead of “gaus+gaus”). It does not seems to work with general functions (ex: “f1+f2” and not “f1(0)+f1(3)” see below)

Now I run the small test below, after I realized some of my fit results looked strange:

  gROOT->Reset();
  TF1 *f1 = new TF1("f1","[0]*TMath::Voigt(x-[1],[2],[3],4)",-4,8); 
  TF1 *f2 = new TF1("f2","pol1",-4,8);
  TF1 *f = new TF1("f","f1+f2",-4,8); 
  TF1 *g = new TF1("g","f2+f1",-4,8); 
  f->SetParameters(10,2,1,1,1,-1);
  g->SetParameters(1,-1,10,2,1,1);
  cout << f->GetExpFormula("p") << endl;
  cout << g->GetExpFormula("p") << endl;
  f->Draw("p");
  g->SetLineColor(2);
  g->Draw("same");

The formula obtained with GetExpFormula(“p”) is:

([0]*TMath::Voigt(x-[1],[2],[3],4))+pol1
pol1+([2]*TMath::Voigt(x-[3],[4],[5],4))

which is what one would expect. Although the graphical results are different:

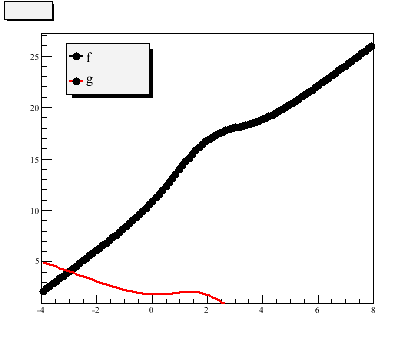
and the strangest thing for me is that is “f” which is wrong.

Finally adding explicitly pol1(4) or pol1(0) instead of f2 in respectively f et g solved the issue… as expected of course.

I guess this is somehow a normal behavior but then I came to the conclusion that is it possible to automatically add user defined functions generated from formulas but not predefined functions. I am right?
For now on I will then explicitly defined my polynomial with “[0]+[1]*x+…”. But maybe it is possible to have ROOT directly doing this ?

Best regards
Julien

PS: forgot to say: I am using ROOT 5.28 on a linux box (ubuntu 10.04)

3

Hi,

You should first see at the documentation in root.cern.ch/root/html/TF1.html and in particular

For general cases I would define by TF1 using a functor as described in the above documentation.

Lorenzo