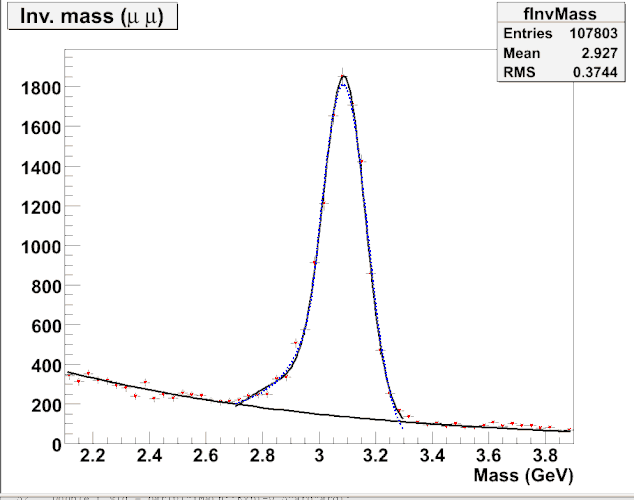
Hello 
I’m writing a little macro in order to compare two kind of fit: crystal ball and a combination of 2 Gaussians. The macro works fine but for the integral the value seems to be not good. The result of the integral is about 438 for the two methods. When I look the plot and the fit I expect a higher value.
Here is the code
[code]#include “TMath.h”
#include “TFile.h”
#include “TH1.h”
#include “TF1.h”
#include “Riostream.h”
#include “Riostream.h”
#include <math.h>
#include “TStyle.h”
#include “TCanvas.h”
#include <TROOT.h>
Bool_t reject;
//Crystal ball function for signal, parameters are 0:alpha,1:n,2:mean,3:sigma,4:normalization;
Double_t CrystalBall(Double_t *x,Double_t *par) {
Double_t t = (x[0]-par[2])/par[3];
if (par[0] < 0) t = -t;
Double_t absAlpha = fabs((Double_t)par[0]);
if (t >= -absAlpha) {
return par[4]exp(-0.5tt);
}
else {
Double_t a = TMath::Power(par[1]/absAlpha,par[1])exp(-0.5absAlphaabsAlpha);
Double_t b= par[1]/absAlpha - absAlpha;
return par[4]*(a/TMath::Power(b - t, par[1]));
}
}
//Exponential background excluding the signal area
Double_t Background(Double_t *x, Double_t *par)
{
if (reject && x[0] > 2.7 && x[0] < 3.3) {
TF1::RejectPoint();
return 0;
}
return exp(-(x[0]-par[0]));
}
//Superposition of 2 gaussians
Double_t G1(Double_t *x, Double_t *par)
{
Double_t arg = 0;
if (par[2]) arg = (x[0] - par[1])/par[2];
Double_t sig = par[0]TMath::Exp(-0.5arg*arg);
return sig;
}
Double_t G2(Double_t *x, Double_t *par)
{
Double_t arg = 0;
if (par[2]) arg = (x[0] - par[1])/par[2];
Double_t sig = par[0]TMath::Exp(-0.5arg*arg);
return sig;
}
Double_t Total(Double_t *x, Double_t *par)
{
Double_t tot = G1(x,par) + G2(x,&par[3]);
return tot;
}
void FitCB()
{
gStyle->SetCanvasBorderMode(0);
gStyle->SetCanvasColor(kWhite);
gStyle->SetFrameBorderMode(0);
gStyle->SetFrameFillColor(kWhite);
gStyle->SetPalette(1,0);
TFile *f = new TFile(“EM.AOD.root”);
TList *t = new TList();
f->GetObject(“list”,t);
TH1F* hpx = (TH1F*)t->FindObject(“fInvMass”);
TCanvas *c1 = new TCanvas(“c1”,“the fit canvas”,1000,800);
TF1 *func = new TF1(“func”,Background,2,4,1);
func->SetParameters(-0.85,0);
func->SetParNames(“slope”);
//Fit the background
reject = kTRUE;
hpx->Fit(func,“r”);
reject = kFALSE;
//Crytal ball declaration
TF1 *crystal = new TF1(“crystal”,CrystalBall,2.7,3.3,5);
crystal->SetParameters(1,1,3.1,0.08,2000);
crystal->SetParNames("#alpha",“n”,“Mean”,"#sigma",“N”);
hpx->Fit(crystal,“r”);
hpx->Draw();
Int_t npar = 6;
Double_t params[6] = {1500,3.096,0.08,350,3.096,1};
TF1 *theory = new TF1(“theory”,Total,2.7,3.3,npar);
theory->SetParameters(params);
theory->SetParNames(“N G1”,“Mean G1”,"#sigma G1",“N G2”,“Mean G2”,"#sigma G2");
hpx->Fit(“theory”,“r”);
func->Draw(“same”);
theory->Draw(“same”);
crystal->SetLineColor(kBlue);
crystal->SetLineStyle(kDashed);
crystal->Draw(“same”);
Double_t numberOfJpsi = crystal->Integral(2.7,3.3);
cout << “Number of JPsi by the crystal ball method” << endl;
cout << numberOfJpsi << endl;
Double_t numberOfJpsi2 = theory->Integral(2.7,3.3);
cout << “Number of JPsi by the 2 gaussians method” << endl;
cout << numberOfJpsi2 << endl;
Int_t a = hpx->GetXaxis()->FindFixBin(2.7);
Int_t b = hpx->GetXaxis()->FindFixBin(3.3);
Double_t hpxIntegral = hpx->Integral(a,b);
cout << hpxIntegral << endl;
}
[/code]