Single Pole Model Fit converging but looking bad and chi square is too large

[Zaiba_Mushtaq]

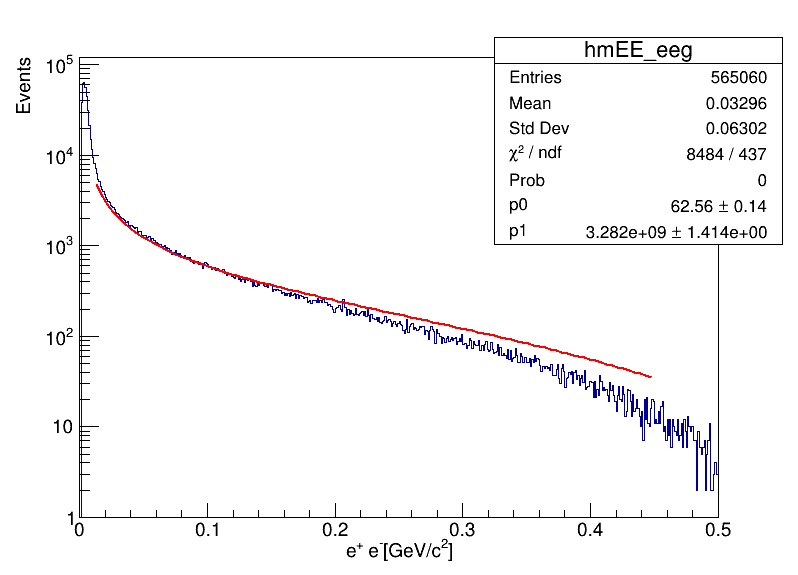
Hello Root Community,
I am seeking guidance on an issue I’ve encountered with my fit results although the fit converges successfully the Chi2 is larger than expected My fit seems like this and the code is attached. Could the issue be related to the initial parameter guesses, or might there be other underlying problems with my approach or data? Any suggestions on what steps I could take to achieve a more reasonable chi-square value would be greatly appreciated. I am including a snippet of the code and a plot of the fit for reference.

[Zaiba_Mushtaq]

Below is my code and histogram. Need suggestions to improve fit.

#include <TFile.h>
#include <TH1D.h>
#include <TF1.h>
#include <TCanvas.h>


    Double_t model(Double_t *x, Double_t *par) {
    double alpha = par[0];
    double lambda2 =par[1];
    double me = 0.000511;
    double m_eta = 0.547;


    double F = 1 / (1 - x[0]*x[0] / lambda2);
    double diff_decay_rate = alpha / x[0] * (1 - 4*me*me/(x[0]*x[0])) * (1 + 2*me*me/(x[0]*x[0])) * pow(1 - ((x[0]*x[0])/m_eta), 3) * (F*F);

    return diff_decay_rate;
}


void test() {

        gStyle->SetOptFit(1111);
        TFile *file1 = TFile::Open("EtaDecay_EEG-results.root", "read");
        TH1D *hmEE_cp_eeg = (TH1D*)file1->Get("hmEE_eeg");

        TCanvas *c1 = new TCanvas("c1", "Form Factor", 800, 600);

        TF1 *f1 = new TF1("f1", model, 0.011, 0.45, 2);
        f1->SetParameter(0, 1000); // Initial guess for parameter alpha
        f1->SetParameter(1, 0.52); // Initial guess for parameter lambda2

        hmEE_cp_eeg->Fit(f1, "R");
        hmEE_cp_eeg->Fit(f1, "R M");
        c1->SetLogy();
        hmEE_cp_eeg->Draw();
        f1->Draw("same"); // Draw the fitting function on top of the histogram

//    file1->Close();
}

[Danilo]

Hi,

It seems from the fit that the model does not describe well your data. Is the value of the chi2 perhaps hinting to that?

Best,
D

[Ako_b]

Hello, @Zaiba_Mushtaq
First of all, based on the information you have provided, I think that you’ve missed m_eta in your formula:

@Zaiba_Mushtaq

* pow(1 - ((x[0]*x[0])/m_eta), 3) *

while I think it should look like this:

double m_eta = 0.547; // GeV/c^2
...
... pow( 1 - ( (x[0]*x[0]) / (m_eta * m_eta) ), 3 ) ...

Secondly, check if the variable x[0] is stored in \text{GeV}/c^2 or \text{GeV}^2/c^4. Even though the axis title says the first case, the confusion might be cause of poor fit. I would advise to double check variables’ unit of measurement and how they should be included in your formula.

Also, you can choose a wider fit region. My formula intuition tells me that the model should more or less be consistent with the peak near zero.

Apart from that, your code snippet seems to be a valid approach in the context of ROOT usage. Maybe you could use RooFit to implement more complex models with ROOT.

In case the model still does not fully describe your data, I would encourage you to discuss this topic with colleagues or experts in the field in other place. As far as I know, this forum is intended to discuss technical problems with ROOT and not consistency of models with data, which actually could be an intricate scientific challenge. However, I would admit that in case with fit results it can be hard to tell if the problem is indeed caused by ROOT.