Dear Edwin,
interesting question! We don’t have this loss function in ROOT, but in C++, you can easily implement the Huber loss function efficiently, mathematically identical to what you have in scikit-learn:
// Sum of Huber loss as implemented in scikit-learn.
double huber_sum_loss(std::size_t n_samples, const double *x, const double *y, const double *params, double epsilon=1.35)
{
double intercept = params[0]; // intercept
double w = params[1]; // slope
double sigma = params[2]; // scale parameter (must be > 0)
double alpha = 0.0001;
int num_outliers = 0;
double outlier_loss = 0.;
double loss_sum = alpha * (w * w); // L1-regularization
for (std::size_t i = 0; i < n_samples; ++i) {
double loss = y[i] - w * x[i] - intercept;
if (std::abs(loss) > epsilon * sigma) {
++num_outliers;
outlier_loss += 2. * epsilon * std::abs(loss);
} else {
loss_sum += loss * loss / sigma;
}
}
loss_sum += n_samples * sigma + outlier_loss - sigma * num_outliers * epsilon * epsilon;
return loss_sum;
}
You can do the numeric minimization with Minuit 2, like in this example macro:
void huber_example()
{
// Data
std::vector<double> g_x{47.5, 47.5, 57.5, 67.5, 67.5};
std::vector<double> g_y{-127.5, 117.5, 112.5, 107.5, 102.5};
double g_epsilon = 1.35; // Huber epsilon (tunable)
cout << "Using Huber epsilon = " << g_epsilon << "\n";
// Create ROOT minimizer (Minuit2/Migrad)
const unsigned int npar = 3; // a, b, sigma
ROOT::Math::Minimizer *min = ROOT::Math::Factory::CreateMinimizer("Minuit2", "Migrad");
// Set tolerances and strategy if you like
min->SetMaxFunctionCalls(100000); // for safety on hard problems
min->SetMaxIterations(10000);
min->SetTolerance(1e-6);
// Create a Functor for the objective function (wrap the C function)
auto loss = [&](const double *params) {
return huber_sum_loss(g_x.size(), g_x.data(), g_y.data(), params, g_epsilon);
};
ROOT::Math::Functor functor(loss, npar);
min->SetFunction(functor);
// Set initial values and step sizes
double step[] = {0.1, 0.1, 0.1};
double variable[] = {0.0, 1.0, 1.0}; // initial guess for a,b,sigma
min->SetVariable(0, "a", variable[0], step[0]);
min->SetVariable(1, "b", variable[1], step[1]);
min->SetVariable(2, "sigma", variable[2], step[2]);
// Run minimization
bool ok = min->Minimize();
if (!ok) {
cout << "Minimization did not converge (Minimize returned false)\n";
}
// Retrieve results
const double *best = min->X();
double a_hat = best[0];
double b_hat = best[1];
double sigma_hat = best[1];
// Estimate errors from minimizer (covariance)
const double *err = min->Errors(); // parameter errors estimate
double a_err = err[0];
double b_err = err[1];
double sigma_err = err[1];
cout << "Fit results (Huber):\n";
cout << " a = " << a_hat << " +/- " << a_err << "\n";
cout << " b = " << b_hat << " +/- " << b_err << "\n";
cout << " sigma = " << sigma_hat << " +/- " << sigma_err << "\n";
cout << "Minimum objective (sum Huber loss) = " << min->MinValue() << "\n";
// For comparison, print OLS fit using simple linear regression (closed form)
// compute ordinary least squares slope/intercept
double sx = 0, sy = 0, sxx = 0, sxy = 0;
for (size_t i = 0; i < g_x.size(); ++i) {
sx += g_x[i];
sy += g_y[i];
sxx += g_x[i] * g_x[i];
sxy += g_x[i] * g_y[i];
}
double n = (double)g_x.size();
double denom = n * sxx - sx * sx;
double ols_b = (n * sxy - sx * sy) / denom;
double ols_a = (sy - ols_b * sx) / n;
cout << "OLS (least-squares) fit:\n";
cout << " a = " << ols_a << " b = " << ols_b << "\n";
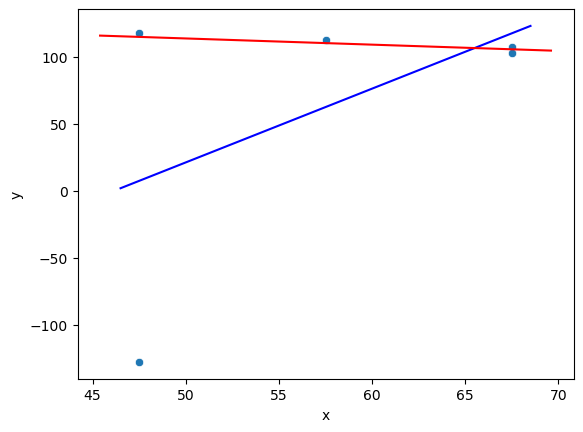
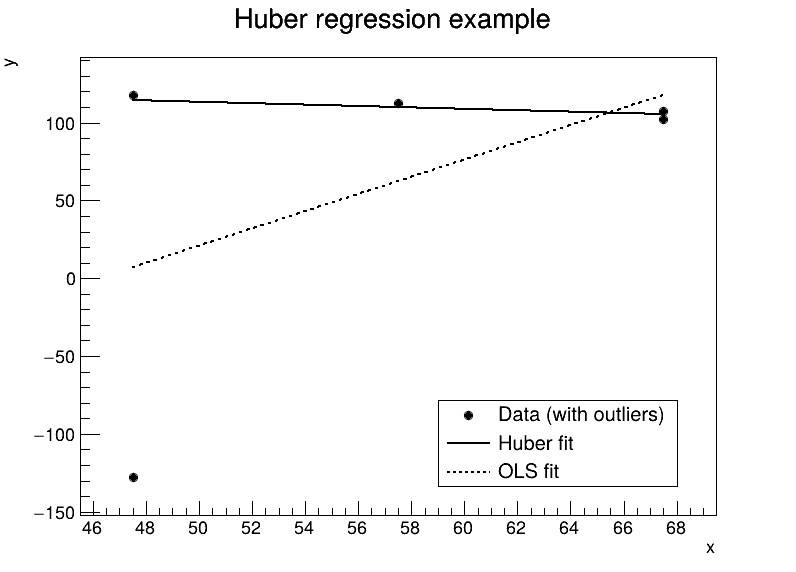
// Draw data and fitted lines
TCanvas *c1 = new TCanvas("c1", "Huber regression example", 800, 600);
c1->cd();
TGraph *gr = new TGraph((int)g_x.size());
for (int i = 0; i < (int)g_x.size(); ++i) {
gr->SetPoint(i, g_x[i], g_y[i]);
}
gr->SetMarkerStyle(20);
gr->SetTitle("Huber regression example; x; y");
gr->Draw("AP");
// Draw Huber fitted line
double xlo = g_x.front();
double xhi = g_x.back();
TLine *hline = new TLine(xlo, a_hat + b_hat * xlo, xhi, a_hat + b_hat * xhi);
hline->SetLineWidth(2);
hline->SetLineStyle(1);
hline->Draw("same");
// Draw OLS fitted line
TLine *lsline = new TLine(xlo, ols_a + ols_b * xlo, xhi, ols_a + ols_b * xhi);
lsline->SetLineWidth(2);
lsline->SetLineStyle(2);
lsline->Draw("same");
// Legend
TLegend *leg = new TLegend(0.55, 0.15, 0.85, 0.30);
leg->AddEntry(gr, "Data (with outliers)", "p");
leg->AddEntry(hline, "Huber fit", "l");
leg->AddEntry(lsline, "OLS fit", "l");
leg->Draw();
// Save to file
c1->SaveAs("huber_fit.png");
// If you want the GUI event loop (interactive), call app.Run();
// For batch runs we can exit now.
delete gr;
delete hline;
delete lsline;
delete leg;
delete c1;
delete min;
}
Output:
Using Huber epsilon = 1.35
Fit results (Huber):
a = 136.752 +/- 8.04162
b = -0.461867 +/- 0.128753
sigma = -0.461867 +/- 0.128753
Minimum objective (sum Huber loss) = 672.318
OLS (least-squares) fit:
a = -253.75 b = 5.5
If it would really help you and your collaborators to have this in ROOT, please feel free to open a GitHub issue with a feature request.
I hope this helps!
Cheers,
Jonas