Root benchmark

ROOT
#1

Hi,
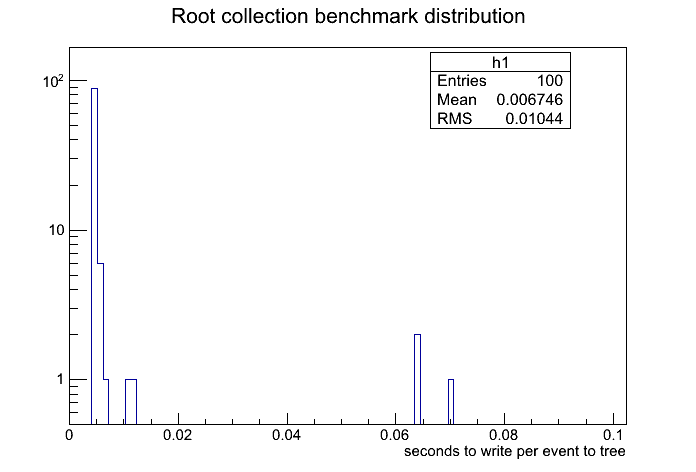
so, I was trying to benchmark root’s latency when collecting data in a standalone application, where the application writes events to a tree (event class is simple, such that it writes time and an array of track data). So it collected about 100 events, where each event had 10000 tracks. I timed how long it took to write each event to the tree. I attached the distribution of those times. So what puzzles me is that there are two peaks, one centered about 0.0047 seconds and the other about 0.064 seconds (granted the latter is a much smaller peak). What I notice though was that the data that contributes to the latter peak occurred after every 30 events written.

I had also noticed that the mean of the latter peak and its interval of occurrence is dependent on what the bufsize is set to when calling:
Tree::Branch(branchname, className, &p_object, bufsize, splitlevel)

So here’s my question:

  1. what is the cause of that latter peak?
  2. what formula can I use (I’m guessing that the size of the events are dependent on this) to set bufsize such that it would minimize the latency when collecting events to a tree?
    rootBench.png696×472 4.05 KB

#2

Hi,

The latter peaks (at a regular interval of entries) is when the basket are flushed to disk (i.e the data accumulated since the last flush is compressed and actually written to the disk).

[quote]2) what formula can I use (I’m guessing that the size of the events are dependent on this) to set bufsize such that it would minimize the latency when collecting events to a tree?[/quote]Well that depends what you are trying to optimize in the end. If you want a quasi constant latency you could use a in-memory TTree (not attached to file) that you write on the file at the very end (thus essentially pushing all the latency to the end of the process). If you really need to reduce the latency but do also need to store the data on the disk on regular basis (and/or can’t afford to push all the latency at the end) you can decrease the number of entries in a cluster (i.e. increase the flush frequency) which mean that they would be less data to process each tick.

Cheers,
Philippe.