Non-relativistic Breit-Wigner and non-relativistic Voigts are implemented as functions in ROOT, though their relativistic versions are not. Would it be possible to implement the relativistic versions? Users implementing their own relativistic Breit-Wigner is quite straight forward (though it would still be useful to have this fairly common function available without having to be implemented by the user), however a relativistic voigt is fairly difficult to implement correctly and would be very helpful to have as an in-built function.
I’ve submitted a pull request for adding the relativistic breit-wigner here https://github.com/root-project/root/pull/9926/commits
For the relativistic breit wigner it’s pretty straight forward since it’s just an analytical function so think the way I’ve implemented it is about as good as it can be.
For the relativistic voigt however it’s a bit more complicated since it’s non analytic.
I’ve produced an implementation below but not submitted a pull request for this. I’m wondering if anyone has any comments and such or thinks this is ok to add? (in particular I’m not sure if the integrator I use is the best for this, or if boost is ok to use in ROOT).
Double_t VoigtRelativistic(Double_t x, Double_t median, Double_t sigma, Double_t lg, Double_t integrationRange=26.615717509251260){ //t=26.615717509251260 gives exp(-t^2)=minimum value stored by double.
Double_t inverse_sSqrt2 = 1/(1.41421356237309504*sigma); //1.41421356237309504=sqrt(2)
Double_t ss = sigma*sigma;
Double_t mm = median*median;
Double_t u1 = (x - median) * inverse_sSqrt2;
Double_t u2 = (x + median) * inverse_sSqrt2;
Double_t a = (lg*median) / (2*ss);
Double_t y = sqrt(mm * (mm+lg*lg));
Double_t k = (0.25397454373696387*a*y)/(ss*sqrt(mm+y)); //0.25397454373696387=sqrt(2)/(pi^(3/2))
auto f = [&](double t) {
Double_t u1Minust = (u1-t);
Double_t u2Minust = (u2-t);
return ( (exp(-t*t)) / (u1Minust*u1Minust * u2Minust*u2Minust + (a*a)) );
};
boost::math::quadrature::tanh_sinh<double> integrator;
Double_t voigt = k* (integrator.integrate(f,-integrationRange,integrationRange));
return voigt;
}
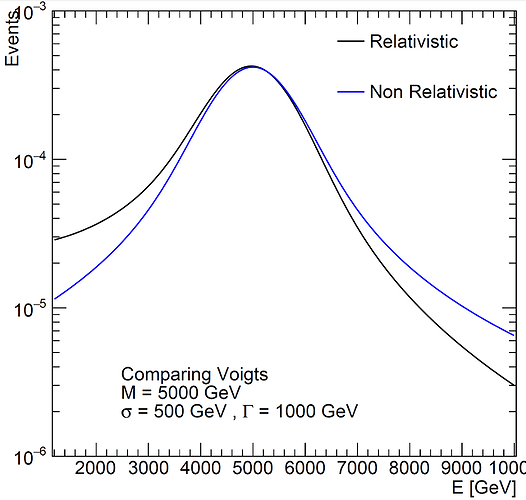
Below is an image comparing the results of this to the current (non relativistic) voigt implemented in ROOT.
Hi,
Thank you for the contribution. For the Relativistic Voigt, one could use the Integrator class of Mathcore, see ROOT: ROOT::Math::IntegratorOneDim Class Reference or the GSL Integrator (ROOT: ROOT::Math::GSLIntegrator Class Reference)
In this case, since we will have this dependency, it is maybe better to have it as a separate class, which could be included in the MathMore library.
Cheers
Lorenzo
Hi @moneta ,
Thank you for the suggestions. I have changed to the IntegratorOneDim class. This requires the dependencies
#include “Math/Integrator.h”
#include “Math/Functor.h”
This works correctly, though there are a lot of options for IntegrationOneDim and I am not sure which if any is the best to use. I have just left it with the default options, though are there any suggestions other than the default (or should I include function arguments for the user to set these options themselves)?
By
it is maybe better to have it as a separate class, which could be included in the MathMore library.
You mean add it is as it’s own .h and .cxx file in MathMore yes? I think it would make more sense in TMath since the non-relativistic Voigt is defined here, but I suppose this is not possible because of the additional dependencies on Math/Integrator.h and Math/Functor.h?
Thanks again for your help
Double_t VoigtRelativistic(Double_t x, Double_t median, Double_t sigma, Double_t lg, Double_t integrationRange=26.615717509251260){ //t=26.615717509251260 gives exp(-t^2)=minimum value stored by double.
Double_t inverse_sSqrt2 = 1/(1.41421356237309504*sigma); //1.41421356237309504=sqrt(2)
Double_t ss = sigma*sigma;
Double_t mm = median*median;
Double_t u1 = (x - median) * inverse_sSqrt2;
Double_t u2 = (x + median) * inverse_sSqrt2;
Double_t a = (lg*median) / (2*ss);
Double_t y = sqrt(mm * (mm+lg*lg));
Double_t k = (0.25397454373696387*a*y)/(ss*sqrt(mm+y)); //0.25397454373696387=sqrt(2)/(pi^(3/2))
auto integrand = [&](Double_t t) {
Double_t u1Minust = (u1-t);
Double_t u2Minust = (u2-t);
return ( (exp(-t*t)) / (u1Minust*u1Minust * u2Minust*u2Minust + (a*a)) );
};
ROOT::Math::Functor1D f(integrand);
ROOT::Math::Integrator integrator(ROOT::Math::IntegrationOneDim::kDEFAULT);
integrator.SetFunction(f);
Double_t voigt = k * integrator.Integral(-integrationRange,integrationRange);
return voigt;
}
Hi,
I would suggest having a separate class, because normally using an integrator requires to allocate some space for the computation. This can be CPU expensive, and in case of repeated evaluation of the function it is better to re-use the integrator class.
For this reason it is better that the Breit-Wigner is a class and for this reason it is better to not include in TMath, but in MathMore with its own .h and .cxx files
Cheers
Lorenzo
Hi @moneta
Thanks, makes sense. I’ll add it as it’s own class in MathMore. Along with this would it be ok to edit the comment in the currently existing Voigt class TMath - source file to mention that there is a relativistic version in MathMore?
Cheers,
Jack
Yes, it will be good to mention this in the Math documentation
Cheers
Lorenzo
Hi @moneta ,
Apologies I’m just checking if the updates I made to my pull request have been lost in the system Add Relativistic Breit Wigner to TMath by JackHLindon · Pull Request #9926 · root-project/root · GitHub
Thanks again for your help,
Jack
See the review comments in the PR. Apologies for the delay