I am looking for a mathematical formula (i.e. something that I can convert into a TF1 later) which describes the total length of random straight tracks inside of a rectangular cuboid (i.e. tracks go in any direction, but they always cross the whole volume, beginning and ending on one of its faces).
I would like to create a TF1 which describes the “probability” of a particular (random) track length.
Maybe @agheata could help you…
Hi,
To fully define the problem, one would need to know the assumptions you make on the starting point and directions. If the starting point is fixed and the direction is uniformly distributed, one could (theoretically) compute the crossing length as function of the direction (which would be a quite complex function already), then derive a probability distribution function in terms of crossing length. If the starting point is also random, one would need to integrate over the fixed point PDF’s. All this would be far from trivial. An easier way would be to numerically sample enough points/directions randomly, compute the crossed length using the TGeoBBox::DistanceFromOutside/Inside functionality, store this in a histogram, normalize the histogram then use it as your probability function. Not as accurate as the analytical approach but as accurate as you need and doable in less than a life time…
Best
The starting and ending points should be completely randomly distributed (well, on different faces, of course, otherwise the track length “inside” would automatically be zero). Maybe a better description is to require a uniform track distribution in 3D (which does not necessarily mean uniform distributions of starting and ending points on faces, I think).
I have been thinking about a “dedicated MC” and creating a histogram but it’s not really what I need.
I would really need a “mathematical formula”. It could also be a sum of “mathematical formulas” using some “numerical parametrization” (where “parameters” could be non-trivial values, requiring some prior numerical integration or “dedicated MC” to find them).
You can of course parameterize the histogram that you would get by doing a dedicated MC to get a usable formula. I can suggest how to do the MC, but not how to deduce the analytical answer.
Well, I think the whole problem is how this “analytical formula” should look like.
But, if you have some appropriate “almost ready to use” MC, it would possibly help a bit, too.
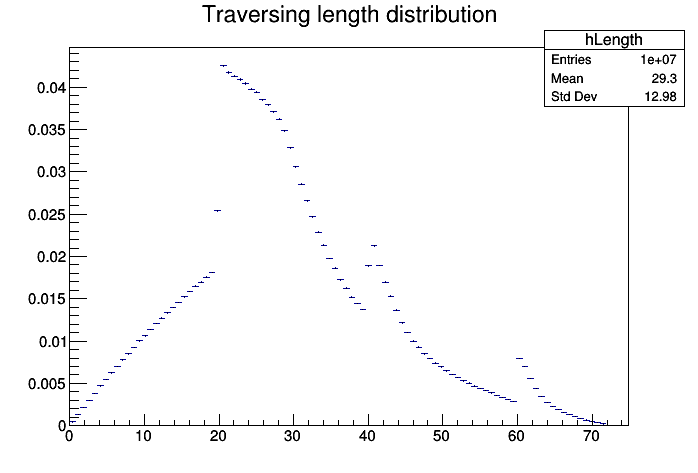
The code below does the MC, and the distribution for a box having (10, 20, 30) as half-lengths looks like in the attached picture. The spikes are to be expected as there are jumps in the distance as the exit point moves from one face to another. That distribution will not be easy to parameterize against arbitrary dimensions of the cuboid, but at least it hints the shape that you expect. Hope it helps.
#include "TMath.h"
#include "TH1.h"
#include "TRandom3.h"
#include "TGeoBBox.h"
void cuboid(double dx, double dy, double dz)
{
// MC for getting the distribution of track length for traversing a cuboid (box)
// Compute the radius of the bounding spere of the cuboid. The maximum traversal
// length is 2*radius
double radius = TMath::Sqrt(dx*dx + dy*dy + dz*dz);
// Make the length distribution histogram. One could increase the binning to have more accuracy.
const int nbins = 100;
TH1F *hLength = new TH1F("hLength", "Traversing length distribution", nbins, 0, 2 * radius);
// Create a box with the desired dimensions
TGeoBBox *cuboid = new TGeoBBox(dx, dy, dz);
// MC generation loop on initial points. More points -> more precision
const size_t nsamples = 1e7;
size_t icross = 0;
double start[3], dir[3];
while (icross < nsamples) {
// Generate the starting point on the bounding sphere. We know the radius, just
// sample phi and theta in spherical coordinates to generate the same number
// of points per surface unit
double phi = TMath::TwoPi() * gRandom->Rndm();
double theta = TMath::ACos(1.-2.*gRandom->Rndm());
// Get corresponding cartesian coordinates for the starting point
start[0] = radius * TMath::Sin(theta) * TMath::Cos(phi);
start[1] = radius * TMath::Sin(theta) * TMath::Sin(phi);
start[2] = radius * TMath::Cos(theta);
// Now generate an isotropic direction (vector norm = 1)
phi = TMath::TwoPi() * gRandom->Rndm();
theta = TMath::ACos(1. - 2.*gRandom->Rndm());
// Get corresponding cartesian coordinates for the starting point
dir[0] = TMath::Sin(theta) * TMath::Cos(phi);
dir[1] = TMath::Sin(theta) * TMath::Sin(phi);
dir[2] = TMath::Cos(theta);
// Now compute the distance for getting into the box
double din = cuboid->DistFromOutside(start, dir, 3);
// Retry if the track misses the box
if (din == TGeoShape::Big()) continue;
icross++;
// Now propagate the track to the surface of the box
for (auto i = 0; i < 3; ++i) start[i] += din * dir[i];
// Compute the distance to exit the box from the new point
double length = cuboid->DistFromInside(start, dir, 3);
// Fill the value in the histogram
hLength->Fill(length);
}
// Normalize and draw the length distribution
hLength->Scale(1./hLength->Integral(), "width");
hLength->Draw();
}
The position of the spikes at 20, 40, 60 are matching the box sizes on the different axis. If you have a box with 2 equal sizes and a third one different, you get only 2 spikes, if you have a cube you get a single spike.
Many thanks for your example. Do you have any idea how to describe this distribution using some “analytical formula”?
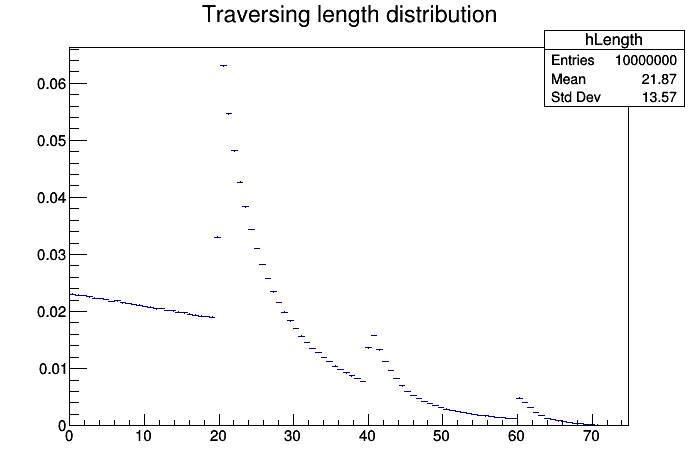
Well, I tried to implement another way of generating random tracks and I got a different picture (no idea how to describe it by any “analytical formula”).
rcuboid.cxx (2.5 KB)
Assuming that this rectangular cuboid is some kind of a fine granularity “particle detector” and the tracks are random “cosmic particles”, which “track length” distribution should one expect (and why)?
Well, I tried to simplify / improve your example and I got yet another distribution.
cuboid.cxx (2.3 KB)
Getting a different distribution is due to changing the input distribution of random rays. The model I proposed where you generate an incoming point randomly on a bounding sphere, then an uncorrelated isotropic direction from that point I thing it emulates best the cosmic ray scenario. In your modified version gRandom->Sphere is ok as simplification, but doing: dir -= start correlates the direction with the starting point, which you shoudn’t. start and dir must be un-correlated.
A parametric function could be defined on ranges: (0, x1), (x1,x2), (x2, x3) and (x3, sqrt(x1x1+x2x2+x3*x3), where x1, x2 and x3 are the ordered sizes of the cuboid. The problem is probably simple to parameterise for a given set x1, x2, x3 (using e.g. polynomials in the fit ranges), but much more difficult for arbitrary sizes.
Yes, in my version of your “cuboid.cxx”, it seems that the requirement that the “starting” and “ending” points of the full track are generated by gRandom->Sphere (and then the “direction = ending point - starting point”) influences the shape of the distribution (in the improved version attached to my previous post above, one can replace “#if 0” with “#if 1” and then one gets your distribution reproduced).
The real problem is how to model these “peaks” analytically (polynomials are not really useful, I would need something that describes them in terms of “means”, “widths” and “heights”).
Unfortunately you cannot model this distribution other than discontinuous, since the actual traversal length has non continuous derivative depending on input direction/angles. Actually the procedure to get the analytical formula involves range-based integration: a ray may cross 2 opposite faces or 2 adjacent ones, depending on the entry point and direction. So no “widths” can be meaningful I’m afraid. What you can try is to understand the correlation of the relative heights of the spikes with the cuboid dimensions. The shape between spikes seems simple to model. If you worry about writing a TF1 with ranges, it is possible:
double xmax = sqrt(x1*x1 + x2*x2 + x3*x3);
TF1 f("f", "(x<[0])?func1:(x<[1])?func2:(x<[2])?func3:func4", 0, xmax);
f.SetParameter(0, x1);
f.SetParameter(1, x2);
f.SetParameter(2, x3);
This topic was automatically closed 14 days after the last reply. New replies are no longer allowed.