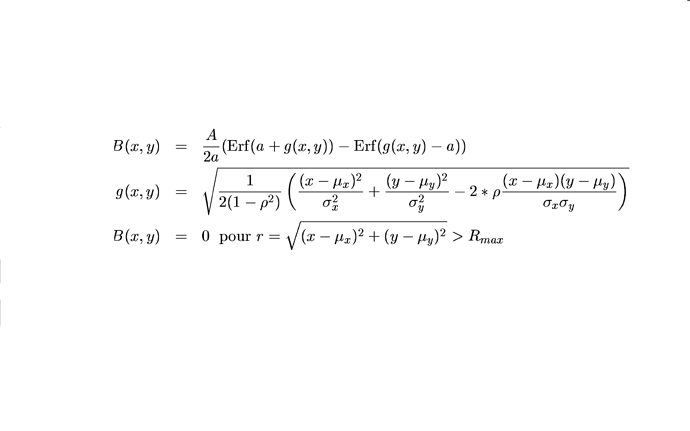Dear all.
I am trying to fit a plot with a function.
The fitting function is the convolution of a 2D Gaussian and a step function in 2D and is reported in the attachment.
The implementation of the fitting function is the following:
Double_t GausErf(Double_t x, Double_t par)
{
//if(par[2] > 0 && par[4] > 0)
if((TMath::Sqrt((x[0]-par[1])(x[0]-par[1])+(x[1]-par[3])(x[1]-par[3])))<1.![]() // Rmax = 1.8 cm
// Rmax = 1.8 cm
{
double rx=0.;
double ry=0.;
double rz=0.;
double den=0;
double g=0;
rx=(x[0]-par[1])/par[2];
ry=(x[1]-par[3])/par[4];
rz=2.par[5]rxry;
den= 1.-par[5]par[5];
g=TMath::Sqrt( (rxrx +ryry - rz)/(2.*den) );
double fitval = (par[0]/ (2.*par[6])) * (TMath::Erf(par[6]+g) - TMath::Erf(g-par[6]));
return fitval;
}
else
return 0;
}
Is there something wrong in this implementation, please?
When I fit in the following way
TH2D h_image = (TH2D)f_image->Get(histoname);
TF2 *g2D=new TF2(“g2d”,GausErf,h_image->GetMean(1)-3,h_image->GetMean(1)+3,h_image->GetMean(2)-3,h_image->GetMean(2)+3,7);
g2D->SetParNames(“Const”,“X_{0}”,"#sigma_{x}",“Y_{0}”,"#sigma_{y}","#rho",“a”);
g2D->SetParameters(0,0,0.5,0,0.5,0.,0);
h_image->Fit(g2D,“R0+”);
I obtain
TF2 *g2D=new TF2(“g2d”,GausErf,h_image->GetMean(1)-lim,h_image->GetMean(1)+lim,h_image->GetMean(2)-lim,h_image->GetMean(2)+lim,7);
g2D->SetParNames(“Const”,“X_{0}”,"#sigma_{x}",“Y_{0}”,"#sigma_{y}","#rho",“a”);
g2D->SetParameters(0,0,0.5,0,0.5,0.,0); // 2010 data
h_image->Fit(g2D,“R0+”);
cout << TMath::Erf(2)<<endl;
I am using root 5.32/01 and the function I am trying to fit with Gaus2DErf is a 2D Gaussian.
Since I will have to fit another function with Gaus2DErf, I am testing the fit on the 2D Gaussian, expectin the term “a” to be zero, but the fit does not work.
Any suggestion/corrections/remarks, please?
Thanks,
regards,
Fra