Problem while fitting graph with 5 gaussians

Newbie
1

Hi everyone!!
I’m currently attempting to fit a graph using 5 Gaussian functions. While I’ve successfully fitted the graph with three Gaussian functions, I’m looking to achieve a fit with five Gaussians, as shown in the below figure.

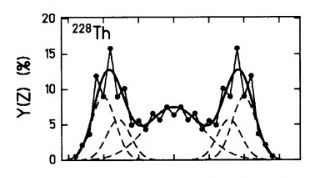
brosa

Below I have attached the code but it’s not yielding the desired outcome.

five_gaus.C (2.3 KB)

Here’s the code for fitting with 3 gaussians which is working perfectly.

> void three_gaus()
> {
> 
> 	TCanvas *c1 = new TCanvas();
> 
>   Double_t x[29] = { 33.83562, 35.75342, 37.94521, 39.58904, 41.78082, 43.42466, 45.34247, 47.26027, 49.17808,51.09589, 53.28767, 55.20548, 56.84932, 59.0411, 60.9589, 62.60274, 64.79452,   66.71233, 68.63014, 70.54795, 72.46575,74.38356, 76.30137, 78.21918, 80.13699, 82.05479, 83.9726, 85.89041, 87.80822 };
>   Double_t y[29] = { 0.4141745, 2.099813, 3.643964, 11.80912, 8.987073, 15.74378, 8.837867, 10.10097, 4.885202,5.584925, 4.312174, 6.561194, 5.571419, 7.39726, 6.265998, 7.3889, 5.552769, 6.534182, 4.276159, 5.539263, 4.971381, 10.0373, 8.906039, 15.6621, 8.897035, 11.70943, 3.676764, 2.122966, 0.4283234 };
>
> 	TGraph *graph = new TGraph(29, x, y);
> 	graph->SetMarkerStyle(8);
> 	graph->Draw("APL");
> 
> 	TF1 *fit1 = new TF1("fit1", "gaus");
> 	fit1->SetLineColor(kMagenta);
>   fit1->SetLineStyle(2);
> 
> 	TF1 *fit2 = new TF1("fit2", "gaus");
> 	fit2->SetLineColor(kGreen);
>   fit2->SetLineStyle(2);
> 
> 	TF1 *fit3 = new TF1("fit3", "gaus");
> 	fit3->SetLineColor(kMagenta);
>   fit3->SetLineStyle(2);
> 
> 	TF1 *total = new TF1("total", "gaus(0)+gaus(3)+gaus(6)", 0, 90);
> 	total->SetLineColor(kBlue);
> 	total->SetParameters(16, 45, 2, 8, 60, 3, 16, 80, 2);
> 	graph->Fit(total, "R+");
> 
>   for (int i = 0; i < 3; ++i)
>   {
>     	fit1->SetParameter(i, total->GetParameter(i));
>     	fit2->SetParameter(i, total->GetParameter(i + 3));
>     	fit3->SetParameter(i, total->GetParameter(i + 6));
>   }
> 
> 	fit1->SetRange(0,90);
> 	fit1->Draw("same");
> 	fit2->SetRange(0,90);
> 	fit2->Draw("same");
> 	fit3->SetRange(0,90);
> 	fit3->Draw("same");
> 
> }

I’d greatly appreciate any guidance or assistance in modifying the code to achieve a successful fit with five Gaussian functions. Thank you in advance for your help!

2

Hi,

Thanks for posting. For any minimisation algorithm, not really specific to ROOT, it could be though to converge reliably on a set of 15 parameter values which is optimal for the sum of 5 gaussians.

My suggestion would be to try to achieve this by starting from sensible starting parameter values, by keeping an eye on the healthy convergence of the fit.

Cheers,
Danilo

1 Like
3

Hi,

fit5gaus.C (2.6 KB)
I suggest this modification of your 5-gaus fit

1 Like
4

Hi Shiva,

I have attached a script that will fit 5 Gaussians to your spectrum but as the saying goes, “be careful what you wish for, you might get it”.

fit_5Gaussians.C (5.3 KB)

Some general remarks:

  1. If your eye can not fit it (“Eyeball Method”), some fancy C++/Python code is not going to save the day
  2. No matter what, your final fit should have all parameters free, otherwise error estimates on the other parameters will be an under estimate.
  3. Make sure the binning of the histogram is not too coarse. The bin-width should be smaller than ~ 0.5 sigma . If that is not the case, apply option "I’ in the fit so that the integrated function is compared to the sum of the histogram counts.
  4. Apply any “knowledge” about the detector setup or physics process to the optimization. Any invariance, conservation law, symmetry should be incorporated in your parametrization. It will reduce the number of free parameters and make the result more robust.

That being said (and knowing nothing about what/how you measured), I observe a symmetry around the third wide Gaussian (x ~= 61). You can incorporate this observation in two ways:

  1. Fit range [30,61] instead of [30,90]
  2. Incorporate constrains in the parametrization.

I did option 2. in the script, enforcing

  • width gauss1 = width gauss 5

  • width gauss 2 = width gauss 4

  • height gauss 1 = height gauss 5

  • height gauss 2 = height gauss 4

Since the binning is rather coarse, I opted to put limits on the parameters
of Gauss 1,2,4 and 5.

Your question is related to ROOT in the following sense. If you look at the code, indexing of the variables is quite involved and error prone. The question now is whether there is a better way in ROOT to link fit parameters.

-Eddy

1 Like
5

Hi Eddy,

your approach is very nice!
Note that w/o the height limits the fit is even better.
Also, the fit option “I” plays no role here.

Smbat

6

Thank You @Danilo, @smgrig, @Eddy_Offermann for helping me out. Really appreciate it. @Eddy_Offermann your detailed explanation really clarified the concept. Thanks again!