Hi @gini
Smear the data means to adding the effect of a resolution broadening your histogram.
What you are doing in your code is not smearing, but just changing the number of counts in each bin.
From your code I see that you have just a file with the number of counts for each bin.
I slightly modified your code to correctly smear the histogram.
I generate a gaussian using the mean and std of h1.
{
gStyle->SetOptStat(2211);
gStyle->SetOptFit(1111);
auto c1 = new TCanvas("c1","Without constraint",800,600);
c1->Divide(2,2);
auto h1 = new TH1D("h1_gaus","Mass (amu);Counts",101.0,39.5,140.5);
auto h2 = new TH1D("h2","h2_Mass_resolution",101.0,39.5,140.5);
auto h3 = new TH1D("h3","h3_Mass_resolution",101.0,39.5,140.5);
h2->SetLineColor(6);
ifstream inp; double x;
inp.open("try.txt");
for (int i=1; i<=100; i++) {
inp >> x;
h1->SetBinContent(i,x);
//loop over the events inside a bin and change it with a resolution of 3.5 with the 2 different methods
for(double j=0;j<x;j++){
h2->Fill( gRandom->Gaus(h1->GetBinCenter(i) ,3.5));
h3->Fill( h1->GetBinCenter(i) + 3.5 * TMath::Sqrt(2.)* TMath::ErfInverse(2. * gRandom->Uniform(1.) - 1.) );
}
}
c1->cd(1);
h1->Fit("gaus","","",44.5, 130.5);
h1->Draw();
c1->cd(2);
h2->Fit("gaus","","",44.5, 130.5);
h2->Draw("");
c1->cd(3);
h1->Draw();
h2->Draw("HIST SAMES");
c1->cd(4);
h3->Draw("");
}
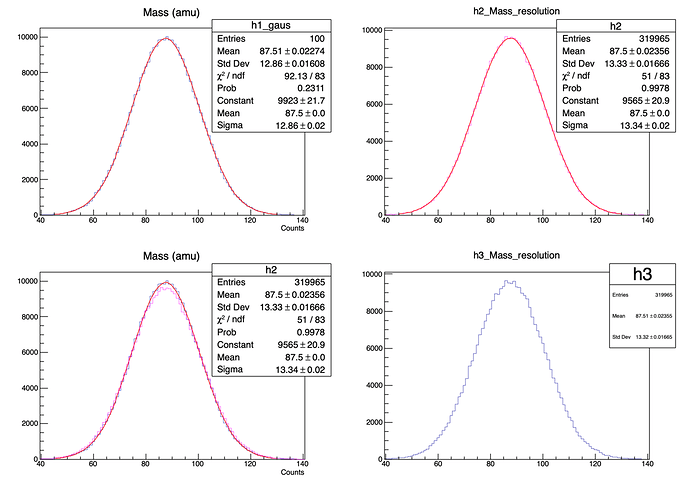
I loop over the bin of h1, and for each bin I generate x events with amu equal to h1->GetBinCenter(i) and for these events I add the effect of a resolution.
The procedure is not really correct, but considering that the bin width is 1/100 of the total range the approximation is fine.
As you can see in the picture the sigma of h2 and h3 is more less equal to sqrt(3.5^2 +12.86^2 ) ~ 13.34, as expected.
I hope to have been clear in my explenation.