Problem in Chi square fit value

Newbie
1

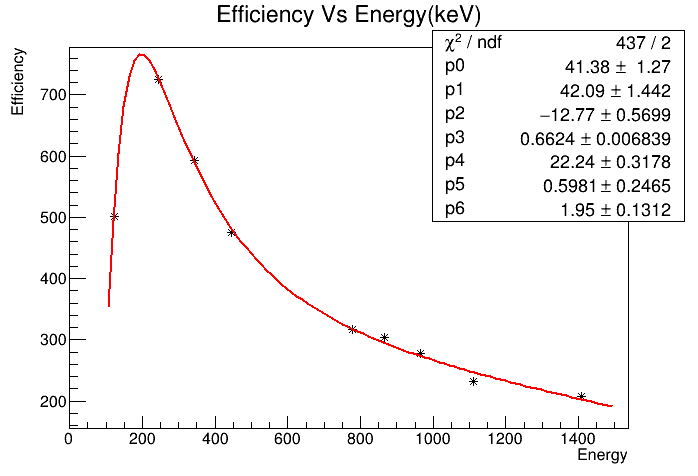
I have drawn a histogram and try to fit it using exponential decay function but the value of chi square is of the order of 10^7.
can you give me any idea about the chi square values?

ROOT Version: Not Provided
Platform: Not Provided
Compiler: Not Provided

2

I’m not sure I understand the question. Could you elaborate and/or post your macro?

3

@jblomer
I am asking about how should i judge my fit. Should I use only chi square value or chi square/ndf value to judge a good or a bad fit?

4

Perhaps @moneta or @StephanH can provide a hint.

5

You definitely have to normalise the chi2 value. chi2/ndf is a good start (it should be a bit larger than 1), but you can do it more accurately by integrating the chi2 pdf. This will give you the probability to obtain a certain result or a result worse than that. Check this out:
https://root.cern/doc/v620/group__ProbFunc.html#gae07ba00b57c524cfbbc9923cdff3f9b0

6

Thanks @StephanH
What if chi square has a value of 0.0025 and chi square/ndf = 0.0025/4?
What if chi square is slightly lesser than 1?

7

Well, compute the probabilities with the function I gave you, or have a look at the distribution in e.g.

chi2/ndf = 0.0025/4 is way too good to come from random fluctuations. That looks like you have a fit function that is way to good at following all the points (e.g. a 5th-degree polynomial for 6 data points - that can obviously fit the points almost perfectly).

8

Thanks @StephanH
Could you check whether this curve is good fit or not?

effvsEnergy
effvsEnergy698×476 7.68 KB

9

Well, if you used the function I mentioned above, you would find that the probability to find such result or a fit that’s worse is 1.E-95. So no, it’s a bad fit.
However, visually, it looks somehow ok. That is an indication that the errors of your points are either wrong or non-existent.

1 Like
10

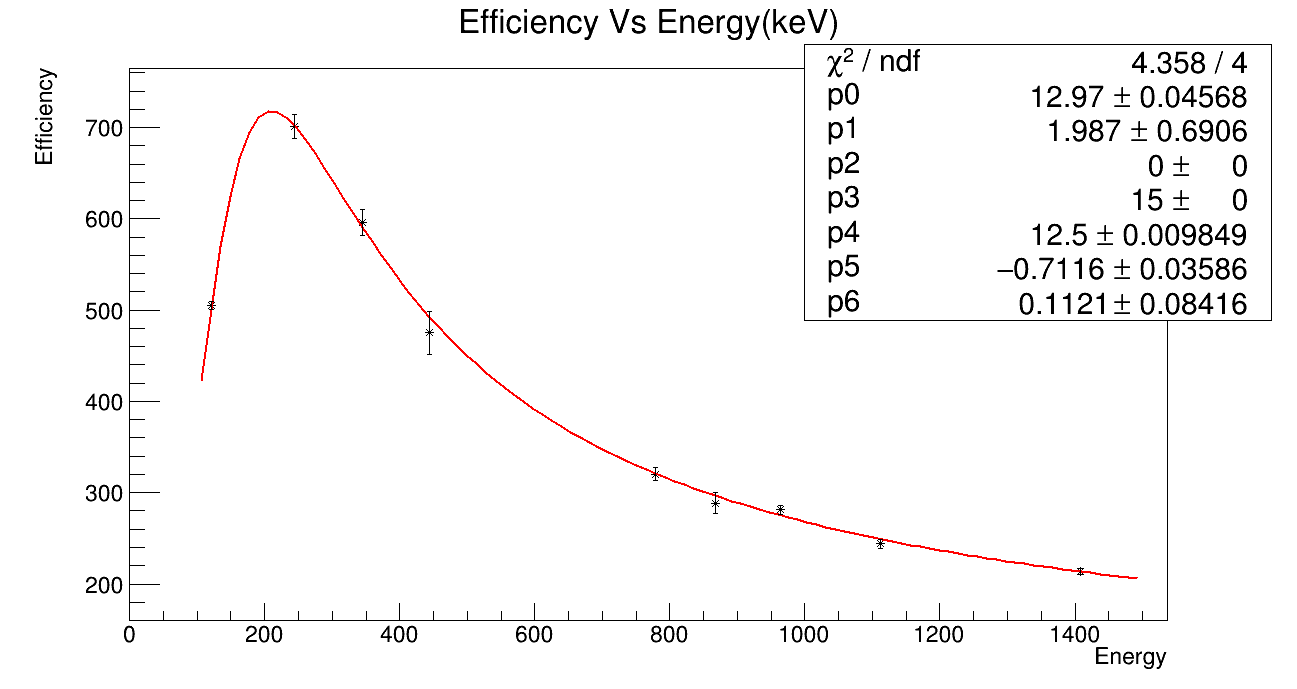
Hi @StephanH

ef
ef1297×689 13.7 KB

The above shown graph(drawn with error bars) shows the value of chi square/ndf = 4.358/4.
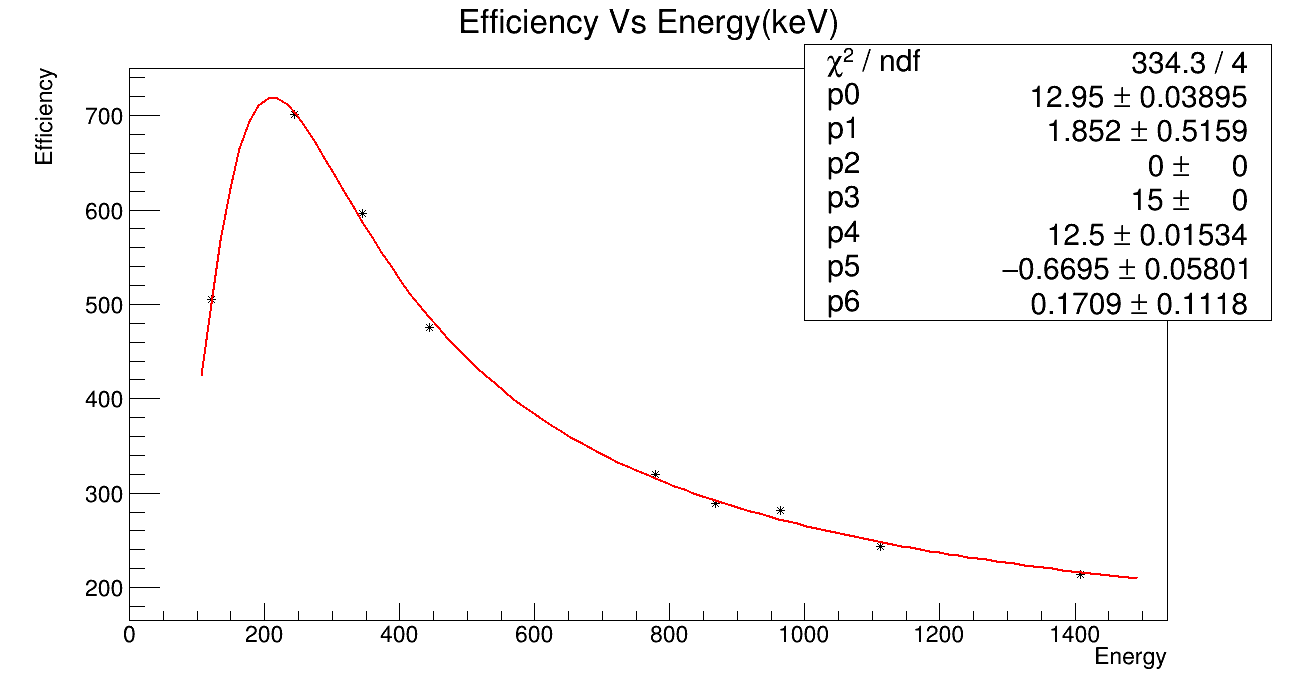
But if I remove the error bars the value of chi square/ndf changes drastically to 334.3/4.
ef1
ef11297×689 13.5 KB

Could you please elaborate on it?

11

Try to fit the graph with error bars using the “W” fit option.

12

Thanks @Wile_E_Coyote.
It is showing higher values of chi square as it ignores the error bars for every point.
Can I assume it as a bad fit?

13

Before you fit, you need to get errors that you can trust in. Just looking at the upper graph that you showed, they errors and also the fit look somehow reasonable. Much better, anyway, than anything that you had before. But you really first have to get reasonable errors, and then you can fit and run statistical tests.

By the way:
The chi^2 probability for the upper fit is
TMath::Prob(4.358, 4) = 0.36, so not that bad.

14

@StephanH
Can you please provide me code for finding the chi square probability so that each time I can find on my own.

15

TF1::GetChisquare
TF1::GetNDF

16

It’s here:

Or here:

And the values that you have to insert you get from here:

17

@StephanH

https://mathworld.wolfram.com/Chi-SquaredDistribution.html
Actually it is given as P(r/2, chi^2/2) but you have written opposite values of arguments.

18

TMath::Prob