Dear experts,
I have been working for some time on fitting a 2D histogram with a paraboloid in a certain range.
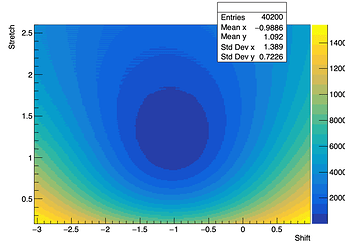
The problem is the following: I have a TH2F which consists of chi-square values in a two-parameter space. The x-axis is a shift applied to a histogram, and the y-axis are stretches. In theory, the chi2 value near the minimum should be a paraboloid (because we are working with two parameters) with this equation (sorry I write the equation this way, I dont know if the Forum supports LaTeX equations):
f(x, y; sigmax, sigmay) = a + 1/(1-rho^2) * ( ((x-x0)/sigmax)^2 + ((y-y0)/sigmay)^2 - 2 rho ((x-x0)/sigmax) ((y-y0)/sigmay) )
where rho = cov(x,y)/(sigmax*sigmay)
So, what I need to do is to fit a histogram (in the figure theres a simple example of the histogram) on a certain range using that equation, in order to get the sigmax and sigmay of the parameters
I used the TH1::Fit() method to fit the histogram, gave all the parameters very sensible starting values but the fit does not even gives the x0 and y0 parameters correctly.
This is the code I used:
double func(double *x, double *p){
double value;
double constant = p[0];
double shift_term = (x[0] - p[1])/p[2];
double stretch_term = (x[1] - p[3])/p[4];
double rho = p[5]/(p[2]*p[4]);
double c = 1.0 - pow(rho, 2);
double mix_term = -2. * rho * ( shift_term * stretch_term );
value = constant + 1/c * (pow(shift_term,2) + pow(stretch_term,2) + mix_term);
return value;
}
void GetXsqErrors(TH2F * hist)
{
// Get minimum bin
int shift_minBin, stretch_minBin, z_minBin;
hist -> GetMinimumBin(shift_minBin, stretch_minBin, z_minBin);
printf("min bin shift = %d\n", shift_minBin);
printf("min bin stretch = %d\n", stretch_minBin);
// Get bin width in x and y
double shift_bin_width = hist->GetXaxis()->GetBinWidth(3);
double stretch_bin_width = hist->GetYaxis()->GetBinWidth(3);
printf("bin width shift = %f\n", shift_bin_width);
printf("bin width stretch = %f\n", stretch_bin_width);
// Get bin center of minimum bin in x and y
double shift_min_bin_center = hist->GetXaxis()->GetBinCenter(shift_minBin);
double stretch_min_bin_center = hist->GetYaxis()->GetBinCenter(stretch_minBin);
printf("shift_min_bin_center = %f\n", shift_min_bin_center);
printf("stretch_min_bin_center = %f\n", stretch_min_bin_center);
// Fit range
double shift_fit_range_min = shift_min_bin_center - 10*shift_bin_width;
double stretch_fit_range_min = stretch_min_bin_center - 20*stretch_bin_width;
double shift_fit_range_max = shift_min_bin_center + 10*shift_bin_width;
double stretch_fit_range_max = stretch_min_bin_center + 20*stretch_bin_width;
printf("shift_fit_range_min = %f\n", shift_fit_range_min);
printf("shift_fit_range_min = %f\n", shift_fit_range_max);
printf("stretch_fit_range_min = %f\n", stretch_fit_range_min);
printf("stretch_fit_range_max = %f\n", stretch_fit_range_max);
TF2 * myfit = new TF2("myfit",
func,
shift_fit_range_min, shift_fit_range_max,
stretch_fit_range_min, stretch_fit_range_max,
6
);
cout << "Constant hist = " << hist->GetMinimum() << endl;
cout << "x0 hist = " << shift_min_bin_center << endl;
cout << "sigma x hist = " << hist->GetStdDev(1) << endl;
cout << "y0 hist = " << stretch_min_bin_center << endl;
cout << "sigma y hist = " << hist->GetStdDev(2) << endl;
cout << "cov hist = " << hist->GetCovariance() << endl;
myfit -> SetParName(0, "Constant");
myfit -> SetParameter(0, hist->GetMinimum());
myfit -> SetParName(1, "x0");
myfit -> SetParameter(1, shift_min_bin_center);
myfit -> SetParName(2, "sigma_x");
myfit -> SetParameter(2, hist->GetStdDev(1));
myfit -> SetParName(3, "y0");
myfit -> SetParameter(3, stretch_min_bin_center);
myfit -> SetParName(4, "sigma_y");
myfit -> SetParameter(4, hist->GetStdDev(2));
myfit -> SetParName(5, "covariance");
myfit -> SetParameter(5, hist->GetCovariance());
// z = a0 + a1*x + a2*x^2 + a3*y + a4*y^2 + a5*x*y
// myfit -> SetParName(0, "a0");
// myfit -> SetParName(1, "a1");
// myfit -> SetParName(2, "a2");
// myfit -> SetParName(3, "a3");
// myfit -> SetParName(4, "a4");
// myfit -> SetParName(5, "a5");
hist -> Fit(myfit, "R 0");
double xmin;
double ymin;
// cout << "fit result = " << (int)r << endl;
cout << "minimum value from fit = " << myfit -> GetMinimumXY(xmin, ymin) << endl;
cout << "minX value from fit = " << xmin << endl;
cout << "minY value from fit = " << ymin << endl;
cout << "minimum value from hist = " << hist -> GetMinimum() << endl;
TCanvas * cfit_cont = new TCanvas("cfit_cont", "", 800, 600);
hist -> Draw("cont3");
myfit -> Draw("cont3 same");
}
void smearing () {
// GetHistogram2D function is not important here, since it works well.
TH2F* chiplot2d = GetHistogram2D();
GetXsqErrors(chiplot2d);
TCanvas * c1 = new TCanvas("c1", "", 800, 600);
chiplot2d -> Draw("colz");
}
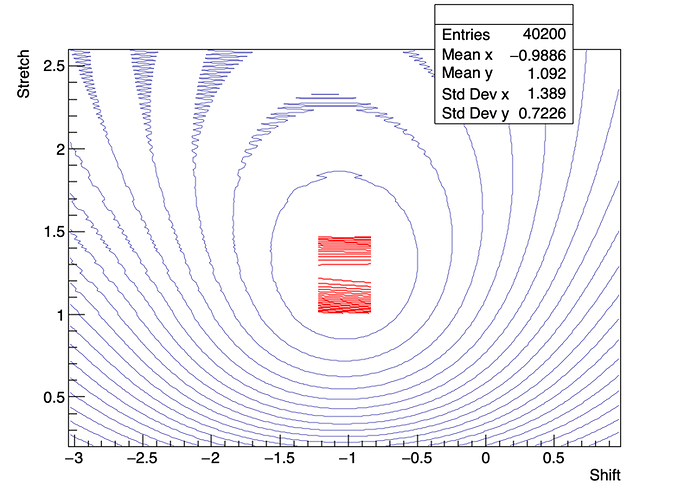
Using this previous code, this is the output I get
The fit is plotted in that subrange in red and the origina histogram in blue contours.
Also, if I change the initial histograms that I compare to compute the chi2 in order they give rise to different minimum values of shift and stretch, the fitting sometimes give good results and sometimes it doesnt, so it seems it’s very unstable. The histogram can be found in this attached file:
hist.root (144.8 KB)
So what I dont understand is why this fitting procedure is so unstable with changes in shift and stretch, and why it does not even give sensible results, this being a very simple problem, with a very good TH2F to fit in the interested range.
Also, if you happen to know an other method I could use to get the parameters uncertainties, e.g. using Roofit or contours fitting, it will be very appreciated if you can point me where I can look for that.
Thank you very much!
Francisco