I was looking for a way to fit one histograms with a linear combination of other histograms. I did come across another forum post which led me to TFractionFitter. What is basically want is h=a(h1)+b(h2)+… , which I did see in the other post. My question was, is it possible to access those weights (a,b,c,…) after having used TFractionFitter?
Thanks
Hi,
You can get the fractions using TFractionFitter::GetResult( par number, value, error).
I attach here an example on how using the TFractionFitter class
Lorenzo
void fractionFitterExample() {
// Example of TFractionFitter class usage
// 1 Dimension only, x is an angle fron 0 to pi
//
// original example from Jerome Baudot May 2010
// https://indico.in2p3.fr/event/2635/contributions/25070/
// modified and updated by L. Moneta
// pointers to the data
TH1F *data; //data histogram
TH1F *mc0; // first MC histogram
TH1F *mc1; // second MC histogram
TH1F *mc2; // third MC histogram
// parameters and functions to generate the data
Int_t Ndata = 1000;
Int_t N0 = 1000;
Int_t N1 = 1000;
Int_t N2 = 1000;
Int_t nBins = 40;
Double_t trueP0 = .05;
Double_t trueP1 = .3;
Double_t trueP2 = 1.-trueP0-trueP1;
// contribution 0
TF1 *f0 = new TF1("f0", "[0]*(1-cos(x))/TMath::Pi()", 0., TMath::Pi());
f0->SetParameter(0,1.);
f0->SetLineColor(2);
Double_t int0 = f0->Integral( 0., TMath::Pi());
// contribution 1
TF1 *f1 = new TF1("f1", "[0]*(1-cos(x)*cos(x))*2./TMath::Pi()", 0., TMath::Pi());
f1->SetParameter(0,1.);
f1->SetLineColor(3);
Double_t int1 = f1->Integral( 0., TMath::Pi());
// contribution 2
TF1 *f2 = new TF1("f2", "[0]*(1+cos(x))/TMath::Pi()", 0., TMath::Pi());
f2->SetParameter(0,1.);
f2->SetLineColor(4);
Double_t int2 = f2->Integral( 0., TMath::Pi());
// generate data
data = new TH1F("data", "Data angle distribution", nBins, 0, TMath::Pi());
data->SetXTitle("x");
data->SetMarkerStyle(20);
data->SetMarkerSize(.7);
data->SetMinimum(0);
TH1F *htruemc0 = new TH1F(*data);
htruemc0->SetLineColor(2);
TH1F *htruemc1 = new TH1F(*data);
htruemc1->SetLineColor(3);
TH1F *htruemc2 = new TH1F(*data);
htruemc2->SetLineColor(4);
Double_t p, x;
for( Int_t i=0; i<Ndata; i++) {
p = gRandom->Uniform();
if( p<trueP0 ) {
x = f0->GetRandom();
htruemc0->Fill(x);
}
else if( p<trueP0+trueP1 ) {
x = f1->GetRandom();
htruemc1->Fill(x);
}
else {
x = f2->GetRandom();
htruemc2->Fill(x);
}
data->Fill( x);
}
// generate MC samples
mc0 = new TH1F("mc0", "MC sample 0 angle distribution", nBins, 0, TMath::Pi());
mc0->SetXTitle("x");
mc0->SetLineColor(2);
mc0->SetMarkerColor(2);
mc0->SetMarkerStyle(24);
mc0->SetMarkerSize(.7);
for( Int_t i=0; i<N0; i++) {
mc0->Fill( f0->GetRandom() );
}
mc1 = new TH1F("mc1", "MC sample 1 angle distribution", nBins, 0, TMath::Pi());
mc1->SetXTitle("x");
mc1->SetLineColor(3);
mc1->SetMarkerColor(3);
mc1->SetMarkerStyle(24);
mc1->SetMarkerSize(.7);
for( Int_t i=0; i<N1; i++) {
mc1->Fill( f1->GetRandom() );
}
mc2 = new TH1F("mc2", "MC sample 2 angle distribution", nBins, 0, TMath::Pi());
mc2->SetXTitle("x");
mc2->SetLineColor(4);
mc2->SetMarkerColor(4);
mc2->SetMarkerStyle(24);
mc2->SetMarkerSize(.7);
for( Int_t i=0; i<N2; i++) {
mc2->Fill( f2->GetRandom() );
}
// FractionFitter
TObjArray *mc = new TObjArray(3); // MC histograms are put in this array
mc->Add(mc0);
mc->Add(mc1);
mc->Add(mc2);
TFractionFitter* fit = new TFractionFitter(data, mc); // initialise
fit->Constrain(0,0.0,1.0); // constrain fraction 1 to be between 0 and 1
fit->Constrain(1,0.0,1.0); // constrain fraction 1 to be between 0 and 1
fit->Constrain(2,0.0,1.0); // constrain fraction 1 to be between 0 and 1
//fit->SetRangeX(1,15); // use only the first 15 bins in the fit
Int_t status = fit->Fit(); // perform the fit
cout << "fit status: " << status << endl;
// Display
gStyle->SetOptStat(0);
TCanvas * c = new TCanvas("c", "FractionFitter example", 700, 700);
c->Divide(2,2);
c->cd(1);
auto oldTitle = f0->GetTitle();
f0->SetTitle("Original MC distributions");
f0->DrawCopy();
f0->SetTitle(oldTitle);
f1->DrawCopy("same");
f2->DrawCopy("same");
c->cd(2);
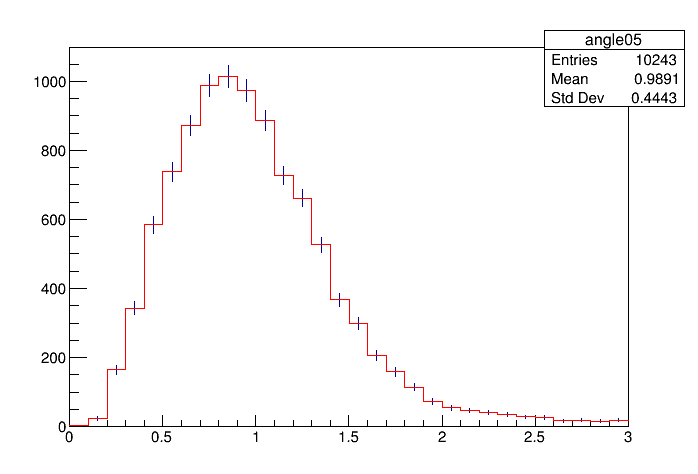
data->SetTitle("Data distribution with true contributions");
data->DrawCopy("EP");
htruemc0->Draw("same");
htruemc1->Draw("same");
htruemc2->Draw("same");
c->cd(3);
mc0->SetTitle("MC generated samples with fit predictions");
mc0->Draw("PE");
mc1->Draw("PEsame");
mc2->Draw("PEsame");
if (status == 0) { // check on fit status
auto mcp0 = (TH1F*)fit->GetMCPrediction(0);
mcp0->SetLineColor(2);
mcp0->Draw("same");
auto mcp1 = (TH1F*)fit->GetMCPrediction(1);
mcp1->SetLineColor(3);
mcp1->Draw("same");
auto mcp2 = (TH1F*)fit->GetMCPrediction(2);
mcp2->SetLineColor(4);
mcp2->Draw("same");
}
c->cd(4);
Double_t p0, p1, p2, errP0, errP1, errP2;
TH1F *mcp0, *mcp1, *mcp2;
TLatex l;
l.SetTextSize(.035);
Char_t texte[200];
if (status == 0) { // check on fit status
TH1F* result = (TH1F*) fit->GetPlot();
fit->GetResult( 0, p0, errP0);
printf(" Parameter %d: true %.3f, estim. %.3f +/- %.3f\n", 0, trueP0, p0, errP0);
fit->GetResult( 1, p1, errP1);
printf(" Parameter %d: true %.3f, estim. %.3f +/- %.3f\n", 1, trueP1, p1, errP1);
fit->GetResult( 2, p2, errP2);
printf(" Parameter %d: true %.3f, estim. %.3f +/- %.3f\n", 2, trueP2, p2, errP2);
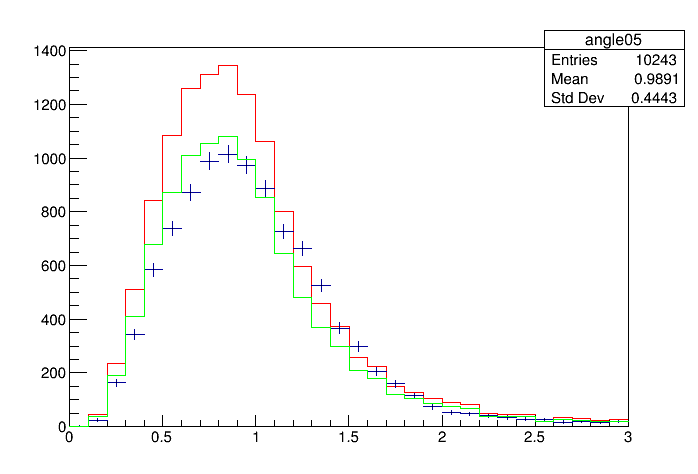
data->SetTitle("Data distribution with fitted contributions");
data->Draw("Ep");
result->Draw("same");
f0->SetParameter(0,Ndata*p0/int0*data->GetBinWidth(1));
f0->SetLineStyle(2);
f0->Draw("same");
f1->SetParameter(0,Ndata*p1/int1*data->GetBinWidth(1));
f1->SetLineStyle(2);
f1->Draw("same");
f2->SetParameter(0,Ndata*p2/int2*data->GetBinWidth(1));
f2->SetLineStyle(2);
f2->Draw("same");
sprintf( texte, "%d: true %.2f, estimated %.2f +/- %.2f\n", 0, trueP0, p0, errP0);
l.DrawTextNDC( .45, .30, texte);
sprintf( texte, "%d: true %.2f, estimated %.2f +/- %.2f\n", 1, trueP1, p1, errP1);
l.DrawTextNDC( .45, .25, texte);
sprintf( texte, "%d: true %.2f, estimated %.2f +/- %.2f\n", 2, trueP2, p2, errP2);
l.DrawTextNDC( .45, .20, texte);
}
}
Thanks for the reply. The p0, p1, p2 in the example, is that just the simple weight (i.e. data = p0mc0 + p1mc1 + p2*mc2 ) of that histogram or something more complicated?
When I use the p0, p1, p2 I get from the fit and do the above mentioned linear combination, I get a different histogram than the fit!
Thanks
Hi,
Yes the p0,p1 and p2 are the fractions for each component.
What do you mean you get a different histogram ? The histogram obtained from the fitted fraction plus the MC components will resample in shape to the one of the data, but it will not be identical. There could also be an overall normalisation term that is not fitted by TFractionFitter.
Lorenzo
I have attached an example below:
This is what I meant by the fractions not matching the linear combination.
Thanks for all your help!
Hi,
What you have make sense. The total normalisation is not fitted by TFractionFitter. It is not an extended fit and for this reason the uncertainty could be slightly under-estimated for this.
Lorenzo
I am sorry but I do not understand what you are trying to say. Can you please explain it to me plainly?
Also, do you think I should use TMinuit to define a function as the linear combination of histograms and then try to do the fit using TMinuit? From what I can tell, the TFractionFitter output looks very similar to that from TMinuit, so is it already using that?
In general, would smoothing the histograms help in case a fit does not converge?
Thanks again!
This topic was automatically closed 14 days after the last reply. New replies are no longer allowed.
