Dear All,
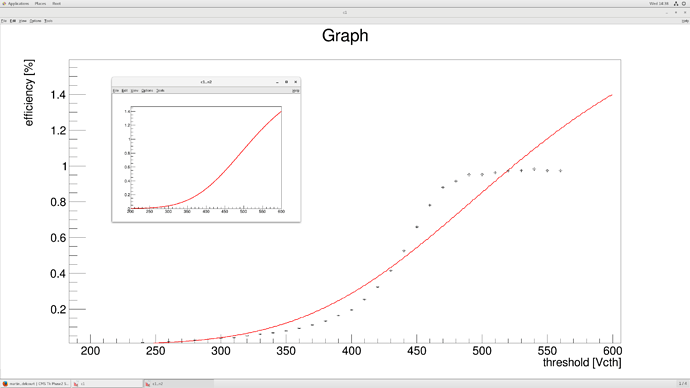
I would like to have the cumulative distribution of a convolution of a Landau(-x) with a gaussian, which I want to use later for a fit. Following the langaus root example, I added another loop around the convolution loop, to do the integration to obtain the cumulative distribution.
My first problem is, that whatever I try to make the landau(-x) it crashes. Second of all, even though I tried making the cumulative distribution, it still looks like the landau*gauss.
The code can be found here:
double lanGausCummulatif(double *x, double *par) {
// Fit parameters:
// par[0] = Width (scale) parameter of Landau density
// par[1] = Most Probable Value parameter of Landau density
// par[2] = Total area (integral -inf to inf, normalization constant)
// par[3] = Width (sigma) of convoluted Gaussian function
//In the Landau distribution (represented by the CERNLIB approximation),
//the maximum is located at x=-0.22278298 with the location parameter=0.
//This shift is corrected within this function, so that the actual
//maximum is identical to the MP parameter.
// Numeric constants
double invSqrd2pi = 0.3989422804014; // (2 pi)^(-1/2)
double mpshift = -0.22278298; // Landau maximum location
// Control constants
double nCsteps = 100.0; // number of convolution steps
double sigmasGauss = 5.0; // convolution extends to +-sc Gaussian sigmas
// Variables
double xx;
double mpc;
double fLandau;
double sum = 0.0;
double step;
// MP shift correction
mpc = par[1] - mpshift * par[0];
// Range of convolution integral
double xlow = x[0] - sigmasGauss * par[3];
double xupp = x[0] + sigmasGauss * par[3];
step = (xupp-xlow) / nCsteps;
double integral = 0.0;
// Convolution integral of Landau and Gaussian by sum
for ( double iVcth = 0.0; iVcth < x[0]; iVcth++ ) {
double differential = 0.0;
for( double iConv = 1.0; iConv <= nCsteps/2; iConv++ ) {
xx = xlow + (iConv-.5) * step;
fLandau = TMath::Landau(xx, mpc, par[0]) / par[0];
//sum += fLandau * TMath::Gaus(x[0], xx, par[3]);
differential += fLandau * TMath::Gaus(iVcth, xx, par[3]);
xx = xupp - (iConv-.5) * step;
fLandau = TMath::Landau(xx, mpc, par[0]) / par[0];
//sum += fLandau * TMath::Gaus(x[0], xx, par[3]);
differential += fLandau * TMath::Gaus(iVcth, xx, par[3]);
}
integral += (par[2] * step * differential * invSqrd2pi / par[3]);
//std::cout << integral << std::endl;
}
//return - (par[2] * step * sum * invSqrd2pi / par[3]);
return integral;
}
TF1 * lanGaus() {
// Currently using a Landau in Vcth units, but could use fC and then scale the PreampShaper output
TF1* f = new TF1("f", "lanGausCummulatif", -600, 600, 4);
// Initial parameter values to be checked!
// I set Landau "width" to 9 (is this the same as sigma?)
// MVP is 144
// Total area of the convolution is 1 for now, this is a normalization factor
// Sigma of the gaussian is 6 (CBC3 noise is 6 Vcth units??? To be checked!!!)
f->SetNpx(5000);
f->SetParameters(9, 440, 1, 6);
f->SetParNames("Width","MP","Area","GSigma");
TCanvas *canvas = new TCanvas();
f->Draw();
return f;
}Could someone please give me some hints on this issue?
Thanks in advance,
Nikkie