Dear TMVA users,
I have a very quick question regarding the KS test used to check for overtraining. I have been using the BDT method with the following number of events:
Signal – training events : 21889
Signal – testing events : 21889
Signal – training and testing events: 43778
Background – training events : 53955
Background – testing events : 53955
Background – training and testing events: 107910
And when checking the BDT score distribution for training and test samples (see below), one can easily that the distributions for these two samples are very similar for both signal and background. It is my understanding that the greater the correspondence between the two distributions, the closer to 0.5 the KS tests. And yet, they are still very close to zero. Are these KS test values really significant or am I missing something here?
Thanks,
K.
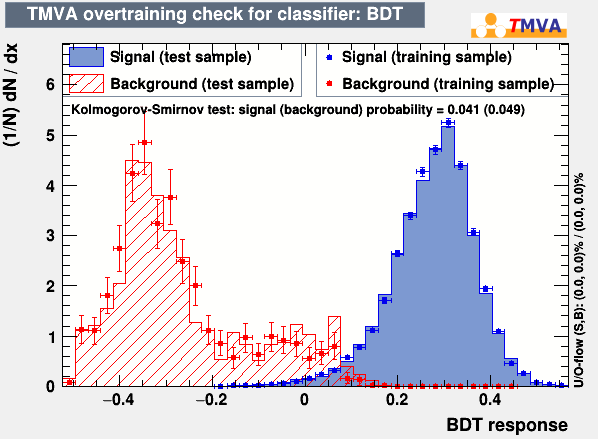
Hi,
Very valid question that I can only begin to answer. It is my understanding that your statement applies to the unbinned case. Then KS value is uniformly distributed between 0 and 1. The binned case then approximates this.
Now, TMVA does not do a straight KS-test, but rather repeats the KS test on a random subsample of the data 1000 times and reports the number of times the individual tests are > 0.5 (normalised to the number of run tests -> optimal value 0.5).
From practical experience, the two distributions need to be very close to each other for the KS test to actually approach 0.5.
You could see if decreasing the number of bins improves the score, or use cross validation (increasing the effective size of the test set).
Cheers,
Kim
1 Like
Thank you Kim for your fast reply. If the optimal case is hard to achieve, I would assume that one could solely rely on their eyes to see if overtraining is significant? I’ll pay around with the samples sizes and see if it improves the KS test values. However, how can I change the binning? I tried to do so directly with the “Editor” view on the plots themselves but I was unsuccessful. Maybe I can change it directly on the function that creates this plot?
Thanks again for your help,
K.
Yes, I think that in many cases this is what it boils down to.
Unfortunately one has to either
- do a retraining for this to take effect since a rederivation of the output histograms are beyond the current capabilities of the
TMVA::Gui, or
- manually evaluate the classifier using the
TMVA::Reader constructing the histograms manually and finally running the KS test on this.
To change the binning for a retraining use (TMVA::gConfig().GetVariablePlotting()).fNbinsMVAoutput = 300;
at the top of the training file.
Cheers,
Kim
Hi,
Can I ask a naive question? I’m puzzled with your description of " KS test on a random subsample of the data 1000 times and reports the number of times the individual tests are > 0.5". Does it really compare to 0.5?
I found that TMVA uses KS test function of TH1 with option “X” (using pseudo-experiment) , in the header:
https://root.cern.ch/root/html608/mvas_8cxx_source.html .
In order to check what happens inside the function, I looked through TH1::KolmogorovTest, I found that it compares the KS values from pseudo-experiments to the value from a direct KS test between the 2 distributions that we want to compare, rather than 0.5, please check the following 2 lines in the source code:
7407 dfmax = TMath::Max(dfmax,TMath::Abs(rsum1-rsum2));
7447 if (dSEXPT>dfmax) prb3 += 1.0;
Thank you,
Cheers,
Linghua
Hi,
Thanks for pointing this out! Yes indeed, the 'X' option performs several single K-S tests. It compares the maximum separation in the sub sample to the maximum separation of entire sample.
Cheers,
Kim
Hi,
If I understand well, with option "X", uncertainties of histograms are not taken into account, when generating pseudo-experiments with the test mva PDF. But do we expect to see the same fluctuation in training and test? For me. it's a bit suspicious.
I have tried with KS test using TMath::KolmogorovProb(z ), which computes z in the formula with maximum separation and uncertainties in case of binned data. it’s impressive that it gives a much better result than the one with pseudo-experiments.
Do you have any idea for this problem?
thank you,
Cheers,
Linghua
Hi,
Sorry no, I personally have limited experience with this K-S test, and I am not aware of any paper discussing the relative merits of the pseudo-experiments in depth.
Maybe @moneta can offer additional insight?
Cheers,
Kim
