Integration of a fit function in a TH1 object

ROOT
1

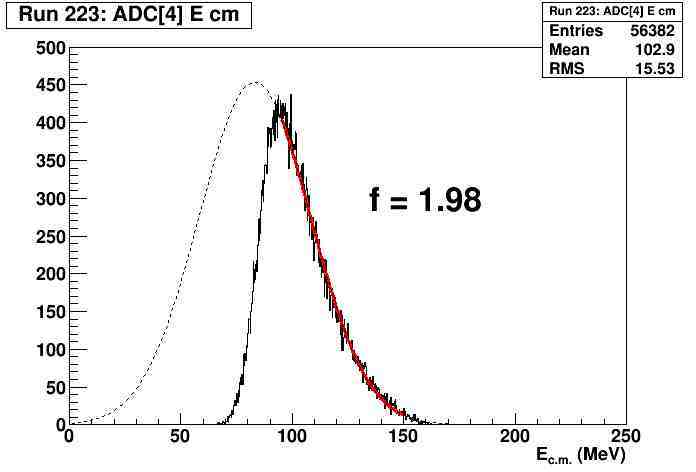
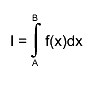I have a experimental energy distribution

h_ffEcm[i] = new TH1F(h_name,h_title,1000,0,250);

which has a high energy threshold; the lower energy part is cut off (see figure 1).

1.jpg696×472 16.9 KB

To estimate how much of the true distribution I’m missing I make a Gaussian fit

fit[i] = new TF1(f_name,"gaus",0,250);

using only the high energy part (red line)

 h_ffEcm[i]->Fit(fit[i],"QB","",95,150);

then I integrate the experimental distribution (h_ffEcm[i]->Integrate()), then the Gaussian distribution (fit[i]->Integral(0,250)), then take the ratio, which becomes my correction factor, a number shown in the figure.

You may notice the factor is close to 2, when a trained eye would say it’s close to 0.5.

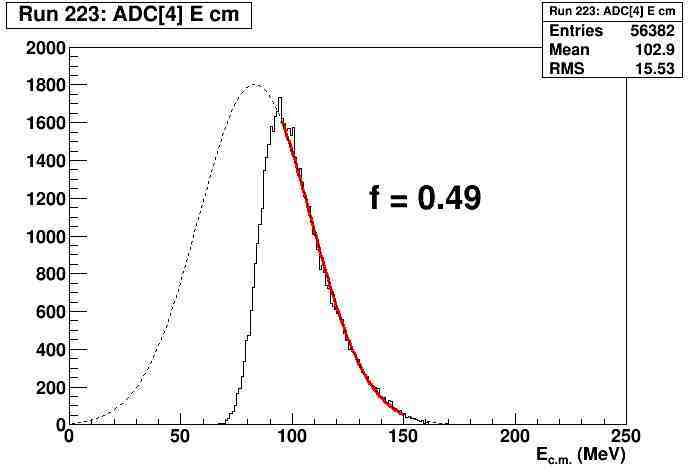
If I rebin the histogram

h_ffEcm[i] = new TH1F(h_name,h_title,250,0,250);

i.e. 1 MeV bins instead of 0.25 MeV bins, then the factor becomes 0.49 (figure 2), which is the correct factor.

2.jpg696×472 16.7 KB

To recap, if I use 0.25 MeV binning of the histogram, the integration of the fit function is 4 times smaller than it should, i.e. in terms of the TH1 constructor the integration is excactly xbins/nbins smaller.

Regardless of binning, h_ffEcm[i]->Integrate()=56382 (also the number of entries).

If nbins=1000, xbins=250, fit[i]->Integral(0,250) = 28501.15.
If nbins=250, xbins=250, fit[i]->Integral(0,250) = .114161.82.

Can anybody explain this behavior, is it a bug or an artifact of mixing objects (TF1, TH1)?

2

Try:
root […] h_ffEcm[i]->Integral(1, h_ffEcm[i]->GetNbinsX(), “width”)
If it helps, see http://root.cern.ch/root/html/TH1.html#TH1:Integral@1 and http://root.cern.ch/root/html/TH1.html#TH1:Integral

3
  1. h_ffEcm[i]->Integral() = 56382
  2. h_ffEcm[i]->Integral(1, h_ffEcm[i]->GetNbinsX(), “width”) = 14095.50

This is OK. 1) is the summing of the bin content, 2) is multiplying the bin content with the bin width and summing. Both are mathematically sound.

But, this is not the issue. The issue is fit[i]->Integral(0,250), which returns different numbers depending on the bin width of the histogram. That doesn’t seem mathematically sound.

If you see root.cern.ch/root/html/TF1.html#TF1:Integral,


(borrowed image from page)

The two integrations,

fit[i]->Integral(0,250) = 28501.15 (nbins=1000 of h_ffEcm[i])
fit[i]->Integral(0,250) = 114161.82 (nbins=250 of h_ffEcm[i])

seem to imply there is something wrong with the dx in the numerical implementation of the integration, right?

In my view, fit[i]->Integral(0,250) = 114161.82 always, regardless of the numbers of bins of h_ffEcm[i]. That is my point.

4

And what does
root […] h_ffEcm[i]->Integral(1, h_ffEcm[i]->GetNbinsX(), “width”)
return when you change the numbers of bins of “h_ffEcm[i]”?

5

h_ffEcm[i]->Integral(1, h_ffEcm[i]->GetNbinsX(), “width”) returns what it should return regardless of the number of bins. Again, that is not the issue I’m trying solve here.

6

Hello Ricardo,

by looking at the y-axis of the two pictures you have posted I am not surprised, that the integral over the fit function gives different results. This is because the bins display the number of entries in the respective x-range. After rebinning the y-value of each bin has increased by a factor of approximately 4. Thus the prefactor of the gaussian fit function should have also increased by a factor of 4.

To get a scale-invariant measure you have to divide the integral over the fit function by the binwidth.

I hope this will lead you to the correct result.

7

I think I now understand this behavior. Basically, the TF1 object is detached from the TH1 object, and I have two options; either divide the TF1 integration by the bin width of the TH1 object, or I multiply the bin content by the bin width of the TH1 object and sum, i.e. use the “width” option mentioned by Pepe Le Pew. I think the former is more transparent, as it involves quantities of one type of object only.

Thank you both.

8

You should use the latter solution (i.e. integrate your histogram using the “width” option and directly compare this value to the integral of the fitted function). This will work for any type of histogram.
The former solution will only work for “fix bin size” histograms.

9

Sorry, I meant the latter, just because of the same reason you mention.