I’m doing research on nuclear physics. What I will be asking is actually some general question.
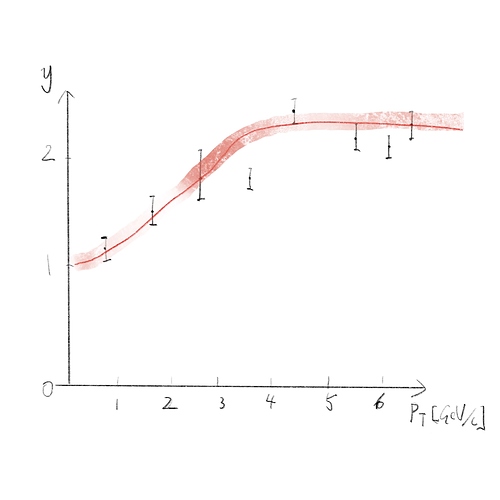
Suppose that I have a set of data with 8 points x={x0,x2…,x7} (in my example, x-axis is transverse momentum), y={y0,…,y7}, and statistical error bars ey={ey0,…ey7}. Using any program that is based on least \chi^2 method and is fed with some fit function f(x,\vec{p})
(here, let’s assume we have 4 parameters), we would get the precise value of p={p0,p1,p2,p3} and their uncertainties err_p={errp0,errp1,errp2,errp3}.
Now here’s the question, how can I draw a band that specifies the statistical uncertainties of this fit function, as illustrated by the red band? Please also give the underlying reason briefly, or maybe some paper that documented this problem well.
I’m asking in ROOT forum because statistically I will be more likely to reach those who can answer. Thanks in advance.