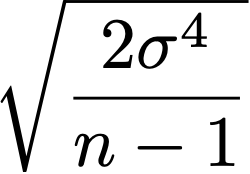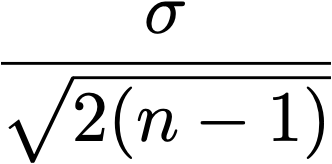How the error of the standard distribution is calculated in root?

gini · August 31, 2022, 10:11am

Hi,

I wonder how the errors of the standard deviation of a histogram are calculated in root?

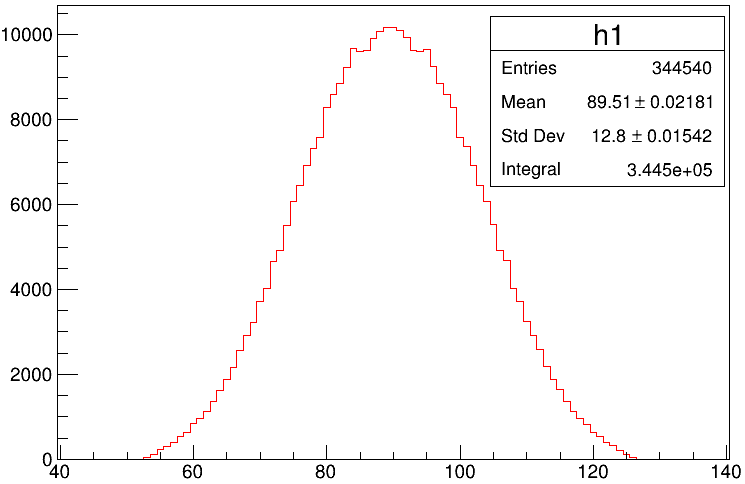
Say for example, in the following histogram (TH1D*h1 = new TH1D(“h1”,“Au_158.62_MeV”,101.,39.5,140.5) attached :

Here the estimation of the mean, error in the mean and the standard deviation are straightforward using the following equation :

eqn

But I don’t understand how the error in the standard deviation is calculated by root. Any help appreciated. Thank you.

jonas · August 31, 2022, 12:11pm

Hi! Thanks for the question.

the uncertainty for the standard deviation is calculated as \sqrt{\frac{\sigma^2}{2n}}, which is the right estimator if the underlying distribution is Gaussian. For a general distribution this is not exact, because the right formula requires the 4th momentum of the distribution, which is not available to the histogram because of the binning.

I got this information from the source code:

github.com

root-project/root/blob/master/hist/hist/src/TH1.cxx#L7536


      
             GetStats(stats);
             if (stats[0] == 0) return 0;
             Int_t ax[3] = {2,4,7};
             Int_t axm = ax[axis%10 - 1];
             x    = stats[axm]/stats[0];
             // for negative stddev (e.g. when having negative weights) - return stdev=0
             stddev2 = TMath::Max( stats[axm+1]/stats[0] -x*x, 0.0 );
             if (axis<10)
                return TMath::Sqrt(stddev2);
             else {
                // The right formula for StdDev error depends on 4th momentum (see Kendall-Stuart Vol 1 pag 243)
                // formula valid for only gaussian distribution ( 4-th momentum =  3 * sigma^4 )
                Double_t neff = GetEffectiveEntries();
                return ( neff > 0 ? TMath::Sqrt(stddev2/(2*neff) ) : 0. );
             }
          }
          
          
////////////////////////////////////////////////////////////////////////////////
          /// Return error of standard deviation estimation for Normal distribution
          ///
          /// Note that the mean value/StdDev is computed using the bins in the currently

This should probably also be written in the docs, so thanks for the reminder!

Dilicus · August 31, 2022, 12:20pm

The variance error is given by

So to have the error on the square root of the variance you just need to evaluate

Edit:
But as said by jonas this formula is valid only for gaussian.

gini · August 31, 2022, 12:39pm

Thank you @jonas and @Dilicus for the clarification.