Hello All,
I’m interested in using the GSLMultiRootFinder to determine the solution (x,y) to the following non-linear system:
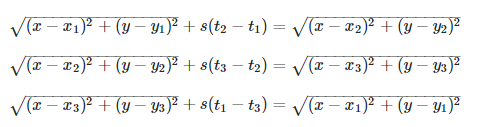
My code is as follows:
#define x1 300000
#define y1 360000
#define x2 210000
#define y2 210000
#define x3 96000
#define y3 360000
#define c 29980000000
void localize(){
ROOT::RDataFrame frame("D","./path/to/data");
auto statn1 = frame.Take<double>("statn1");
auto statn2 = frame.Take<double>("statn2");
auto statn3 = frame.Take<double>("statn3");
TF2 *f1 = new TF2("f1","sqrt((x-[0])^2 + (y-[1])^2) + [2]*([3] - [4]) - sqrt((x-[5])^2 + (y-[6])^2)");
TF2 *f2 = new TF2("f2","sqrt((x-[0])^2 + (y-[1])^2) + [2]*([3] - [4]) - sqrt((x-[5])^2 + (y-[6])^2)");
ROOT::Math::MultiRootFinder rootFinder(0);
int i = 0;
f1->SetParameters(x1,y1,c, statn2->at(i), statn1->at(i), x2,y2);
f2->SetParameters(x2,y2,c, statn3->at(i), statn2->at(i), x3,y3);
ROOT::Math::WrappedMultiTF1 g1(*f1,2);
ROOT::Math::WrappedMultiTF1 g2(*f2,2);
rootFinder.AddFunction(g1);
rootFinder.AddFunction(g2);
rootFinder.SetPrintLevel(1);
double init[2] = {2000, 3200};
rootFinder.Solve(init);
}
Note that the i is a placeholder for what will eventually be a for loop, iterating over all the data in the three .root files.
My problem is, when I run the root finder with the default # of iterations / tolerance values, I get the runtime error the iteration is not making progress.
I tried playing with the # of iterations, and I found that if I set that to something less than 10, I get a different error, exceeded max iterations, reached tolerance is not sufficient. This error continues, even when I increase the tolerance significantly (to a value of, say, something like 0.1 or even 10), or decrease it significantly.
For larger # of iterations values (including extremes like INT_MAX), I continue getting the not making progress “error”.
Any ideas what to do here? I’m certain, mathematically, that the system can be “solved”.
Apologies if this isn’t appropriate for this forum. I’m not entirely familiar with this subject, and I’m not certain if this is a ROOT/coding issue, or perhaps a mathematical issue, or perhaps both.
Please read tips for efficient and successful posting and posting code
ROOT Version: Not Provided
Platform: Not Provided
Compiler: Not Provided