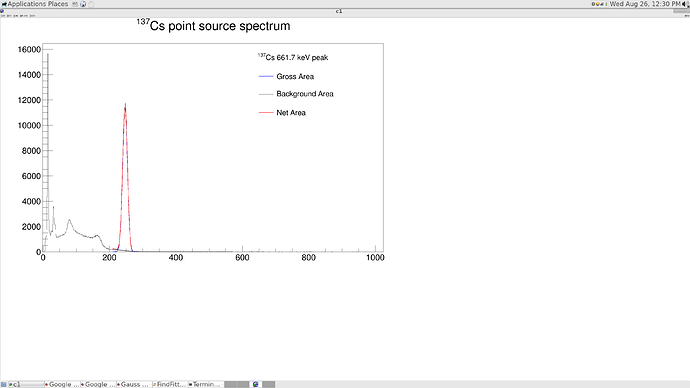
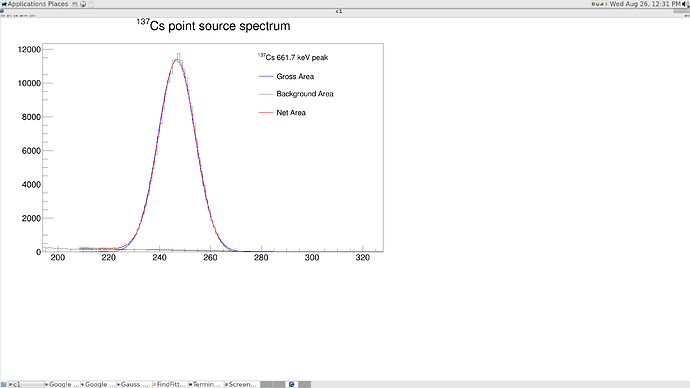
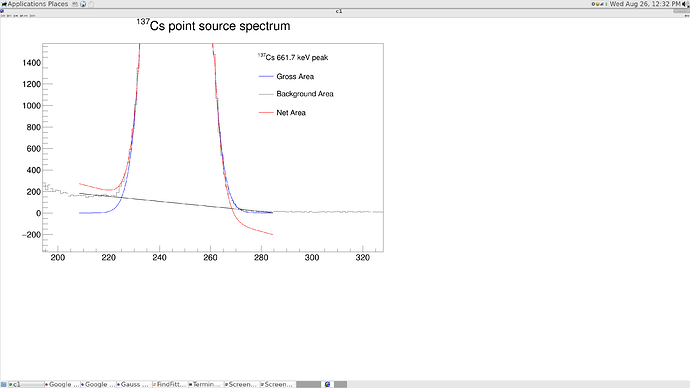
The part for fitting one Gaussian.
void FittingOneGussianFunctions(TH1F *h1, int LL1, int UL1, double & p2){
////////////////////Defining Functions //////////////////////////////////////////////////////////////
//The limits are put t get exact function shapes, so they might be narrow.
int flexibility1=20;
TF1 *g1 = new TF1(“g1”,“gaus”, LL1, UL1 );
TF1 pol1 = new TF1(“pol1”,“pol1”, LL1-flexibility1, UL1+flexibility1 ); //POLYNOMIAL BACKGROUND
TF1 total = new TF1(“total”,“gaus(0)+pol1(3)”, LL1 , UL1 );//TOTAL FUNCTION
/////////////////////////////////////////////////////////////////////////////////////////////////////////
//TH1F h = (TH1F)h1->Clone(“h”);
h1->SetLineColor(kBlack);
g1->SetLineColor(kBlue);
pol1->SetLineColor(kBlack);
total->SetLineColor(kRed);
h1->Fit(g1,“R”);
h1->Fit(pol1,“R+”);
h1->SetStats(000000000);
///////////////////////////////////////////////////////////
// To store the parameter values in to an ARRAY called “par[5]”
double par[5];
g1->GetParameters(&par[0]);
pol1->GetParameters(&par[3]);
total->SetParameters(par); //first get the parameter from g1 and pol1 , then set them for total function as parameters.
h1->Fit(total,“R+”); //Now, I am able to fit and draw this function since I assigned its values which were taken from the first gaussian and pol1 fits
//double chi2 = fitting->GetChisquare();
// value of the first parameter
double p0 = g1->GetParameter(0); //height of gaussian
double p1 = g1->GetParameter(1); //mean value of gaussian
p2 = g1->GetParameter(2); //if this is sigma, width of gaussian=8sigma
cout<<"height value from fit= "<<p0 << endl;
cout<<"mean value from fit= " <<p1 <<endl;
cout<<"sigma value from fit= " <<p2 <<endl;
cout<<"FWHM from fit= "<<2.35p2 <<endl;
////////////////
double p3 = pol1->GetParameter(0);
double p4 = pol1->GetParameter(1);
// error of the first parameter
double e0 = g1->GetParError(0);
double e1 = g1->GetParError(1);
double e2 = g1->GetParError(2);
//////////////////////////////
double e3 = pol1->GetParError(0);
double e4 = pol1->GetParError(1);
///////////////////////////////////////////////
//For interested gaussian peak ONLY
double* gaussParameters = new double[3] ;
gaussParameters[0] = p0;
gaussParameters[1] = p1;
gaussParameters[2] = p2;
double* MyConvarienceMatrix =new double[9];
MyConvarienceMatrix[0]=e0 ;
MyConvarienceMatrix[1]=0 ;
MyConvarienceMatrix[2]=0 ;
MyConvarienceMatrix[3]=0 ;
MyConvarienceMatrix[4]=e1 ;
MyConvarienceMatrix[5]=0 ;
MyConvarienceMatrix[6]=0 ;
MyConvarienceMatrix[7]=0 ;
MyConvarienceMatrix[8]=e2 ;
/////////////////////////////
int HistoBinning=1;
double MyIntegral = g1->Integral( p1-3p2, p1+3p2 ) / HistoBinning ; //p4 is mean value and p5 is sigma value. Gauss range is about 8sigma.
double IntegralError = g1-> IntegralError(p1-3p2 , p1 + 3p2 , gaussParameters, MyConvarienceMatrix) / HistoBinning ;
cout<<"Fitting g1 integral and error: " << g1->Integral( p1-3p2, p1+3p2 ) <<"\t"<<IntegralError <<endl;
cout<<"Fitting pol1 integral and error: " << pol1->Integral( p1-3p2, p1+3p2 ) <<endl;
cout<<"Fitting total integral and error: " << total->Integral( p1-3p2, p1+3*p2 ) <<endl;
//SET gaussian ranges for drawing
g1->SetRange(LL1-flexibility1, UL1+flexibility1);
pol1->SetRange(LL1-flexibility1, UL1+flexibility1);
total->SetRange(LL1-flexibility1, UL1+flexibility1);
////////////////////////////////////////
g1->Draw(“same”);
pol1->Draw(“same”);
total->Draw(“same”);
TLegend *legend1 ;
Double_t xm1=0.6, ym1=0.6, xm2=0.8 , ym2=0.88;
legend1 = new TLegend(xm1,ym1,xm2,ym2);
legend1->SetHeader("^{137}Cs 661.7 keV peak");
legend1->AddEntry(g1,“Gross Area”,“l”);
legend1->AddEntry(pol1,“Background Area”,“l”);
legend1->AddEntry(total,“Net Area”,“l”);
legend1->SetBorderSize(0);
legend1->SetTextSize(0.03);
legend1->Draw();
}