I’m trying to do something quite simple in vain. Basically, I’m trying to fit 6th order polynomial to my histogram using Roofit.
Without Roofit, I would do this:
hh.Fit("pol6","", "", 100, 250);
hh.Draw();and it would work nicely. However, with roofit,
TFile* file=m172500;
file->Print(); TH1* hh=file->Get("trigger_cum/Dilepton_Mlb");
RooRealVar x("x", "Mlb",0, 250);
RooDataHist data("data", "", x, hh);
RooRealVar a0("a0", "", 0.166, -100, 100);
RooRealVar a1("a1", "", -0.027, -10, 10);
RooRealVar a2("a2", "", 0.0015, -10, 1);
RooRealVar a3("a3", "", -2.12741e-05, -1, 1);
RooRealVar a4("a4", "", 1.26994e-07, -1, 1);
RooRealVar a5("a5", "", -3.4875e-10, -1, 1);
RooRealVar a6("a6", "", 3.62884e-13, -1, 1);
Pol6 fpol6("p", "", x, a0, a1, a2, a3, a4, a5, a6);
fpol6.fitTo(data, Range(0, 250), Extended(kTRUE));After a bunch of error messages like
[quote][#0] WARNING:Plotting – At observable [x]=212.5 Pol6::p[ x=x a0=a0 a1=a1 a2=a2 a3=a3 a4=a4 a5=a5 a6=a6 ]
p.d.f value is less than zero (-0.733092), forcing value to zero @ x=x=212.5, a0=a0=0.166 +/- 84.147, a1=a1=-0.027 +/- 8.41468, a2=a2=0.0015 +/- 2.65917, a3=a3=-2.12741e-05 +/- 0.841471, a4=a4=1.26994e-07 +/- 0.841471, a5=a5=-3.4875e-10 +/- 0.841471, a6=a6=3.62821e-13 +/- 0.841471
[/quote]
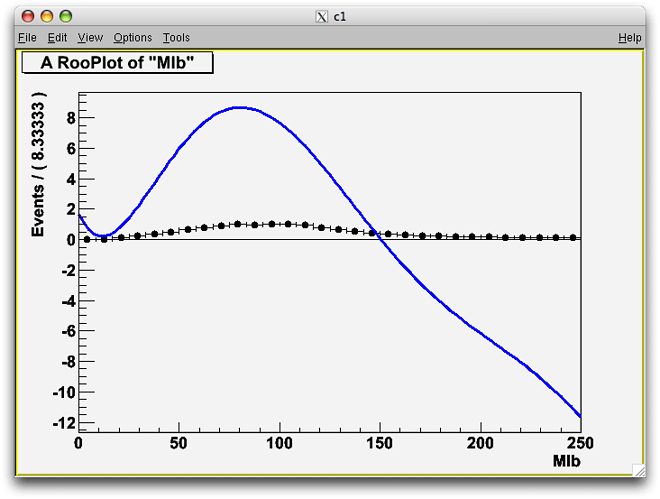
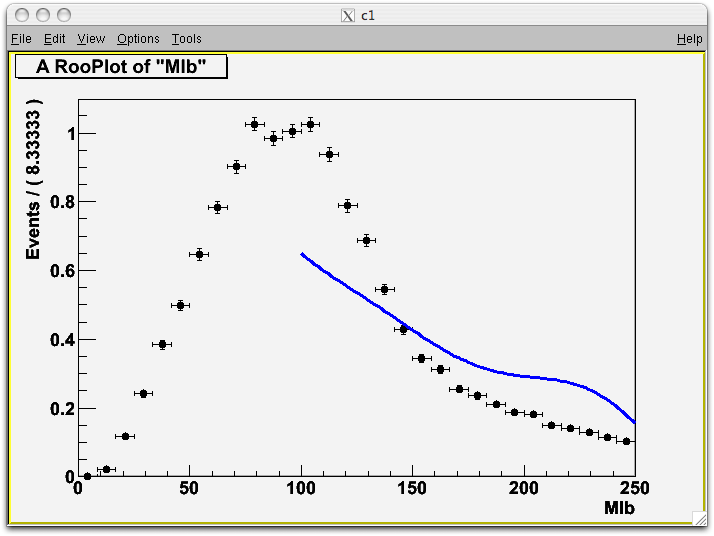
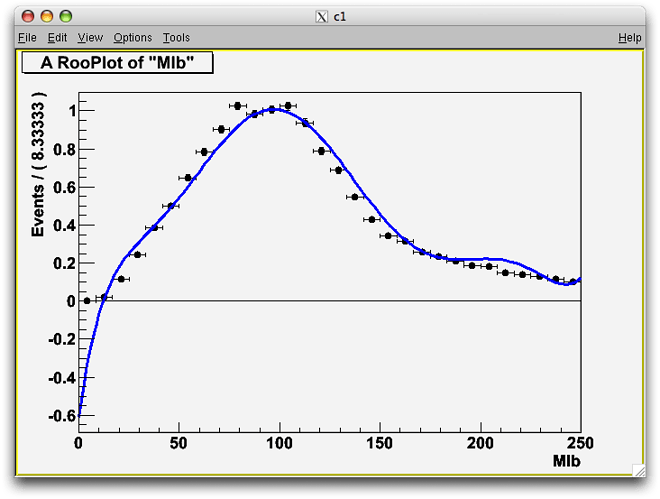
I get a rather poor result as shown in the picture. I think I’m doing something very wrong but I cannot figure what it is. Would you please help understand what’s going on?
Thanks
Akira
hh.root (4.14 KB)