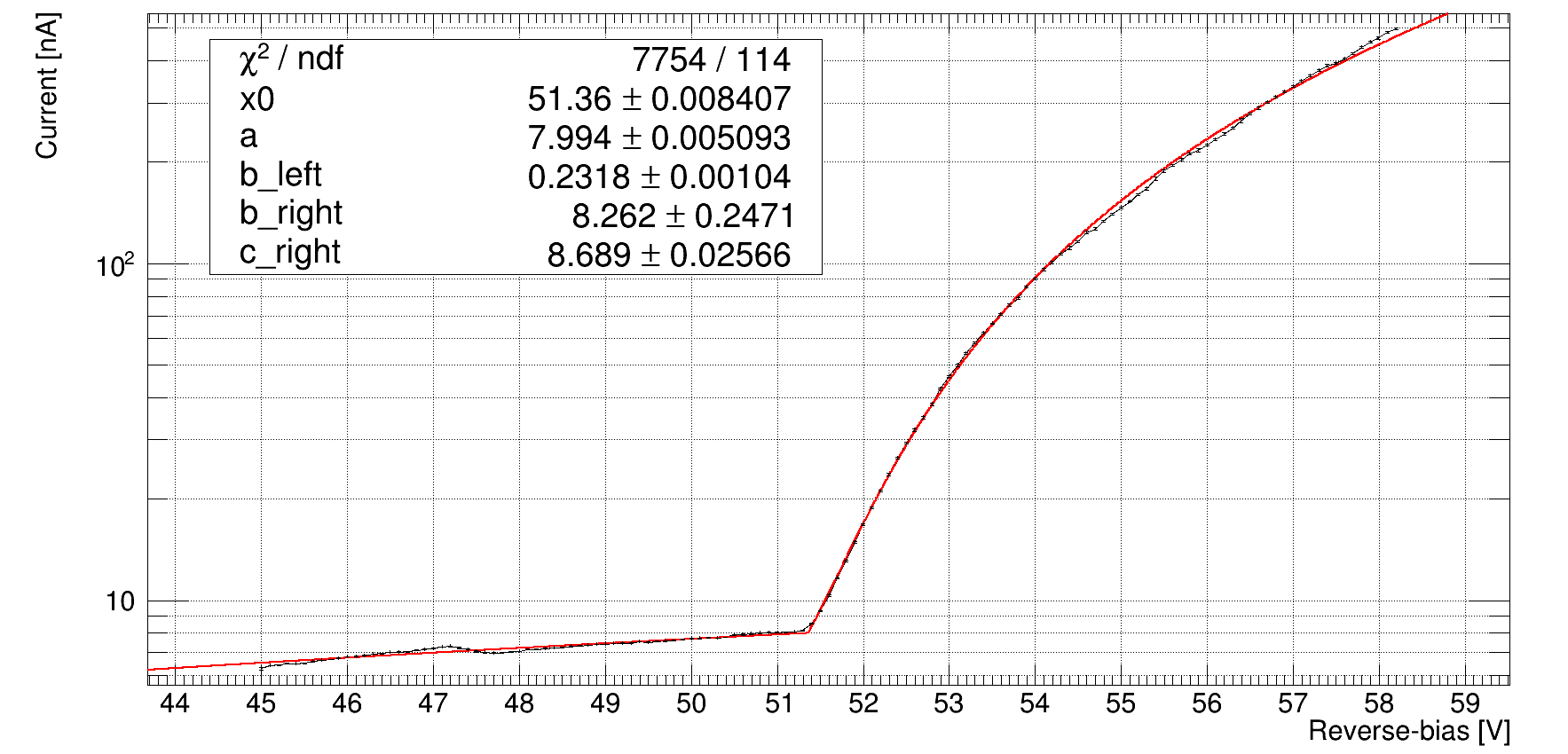
Hi ROOTers,
I acquired some IV curve and im trying to fit them using a combination of linear and parabola fit. The macro used
bool reject = false;
double splitline(const double *x, const double *p) {
// y = a + b * (x - x0) + c * (x - x0) * (x - x0)
double x0 = p[0]; // "point of split"
double a = p[1]; // "left" and "right" (linear and parabolic)
double b_left = p[2]; // "left" (linear)
double b_right = p[3]; // "right" (parabolic)
double c_right = p[4]; // "right" (parabolic)
double dx = x[0] - x0;
// when fitting, exclude points which are close to the "point of split"
if (reject && (dx > -1.075) && (dx < 0.3)) // note: asymmetric range, change it in order to obtain the best chi squared
TF1::RejectPoint();
return (a + ((dx < 0.) ? b_left : b_right + c_right * dx) * dx);
}
void hamamatsu(const char *fname = "1_inversa.txt") {
if (!(fname && fname[0])) return; // just a precaution
TGraphErrors *g = new TGraphErrors(fname);
if (!(g->GetN())) return; // just a precaution
g->Sort(); // just a precaution
g->SetTitle("Curve I-V;Reverse-bias [V];Current [nA]");
g->GetXaxis()->SetNdivisions(1925);
g->GetYaxis()->SetNdivisions(748);
TCanvas *c = new TCanvas("c", "Curve I-V");
c->SetFillColor(0);
c->SetBorderMode(0);
c->SetBorderSize(2);
c->SetFrameBorderMode(0);
c->SetGrid(1, 1);
c->SetTicks(1, 1);
c->SetLogy();
gStyle->SetOptFit(000); // 111 per vedere i parametri di fit
TF1 *f = new TF1("f_splitline", splitline, g->GetX()[0], g->GetX()[(g->GetN() - 1)], 5);
f->SetParNames("x0", "a", "b_left", "b_right", "c_right");
f->SetNpx(8000);
// note: one should always set "reasonable" initial values for all parameters
f->SetParameters((g->GetX()[0] + g->GetX()[(g->GetN() - 1)]) / 2., g->GetY()[0], 0., 0., 0.);
// f->SetParameters(50., 0.1, 0., 10., 10.);
#if 0 /* 0 or 1 */
// try to make the fit more "robust" (when initial parameters are not good)
// f->SetParLimits(0, g->GetX()[0], g->GetX()[(g->GetN() - 1)]); // x0
// f->SetParLimits(1, 0., 1000.); // a >= 0
f->SetParLimits(2, 0., 1000.); // b_left >= 0
f->SetParLimits(3, 0., 1000.); // b_right >= 0
f->SetParLimits(4, 0., 1000.); // c_right >= 0
#endif /* 0 or 1 */
reject = true;
g->Fit(f, "QN"); // first "initial pre-fit"
g->Fit(f, "QN"); // second "initial pre-fit"
g->Fit(f, "QN"); // third "initial pre-fit"
g->Fit(f, "QN"); // fourth "initial pre-fit"
g->Fit(f, ""); // "final fit"
reject = false;
g->Draw("ALP");
}
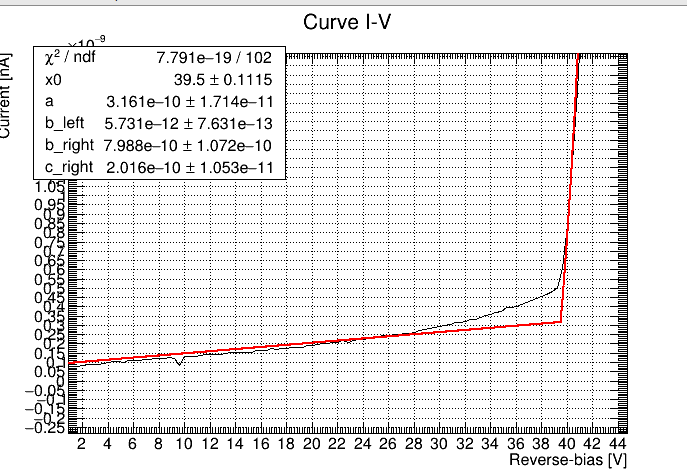
works perfectly for some kind of curve like HPK_S13_anode10_25C_inv.txt (6,5 KB):
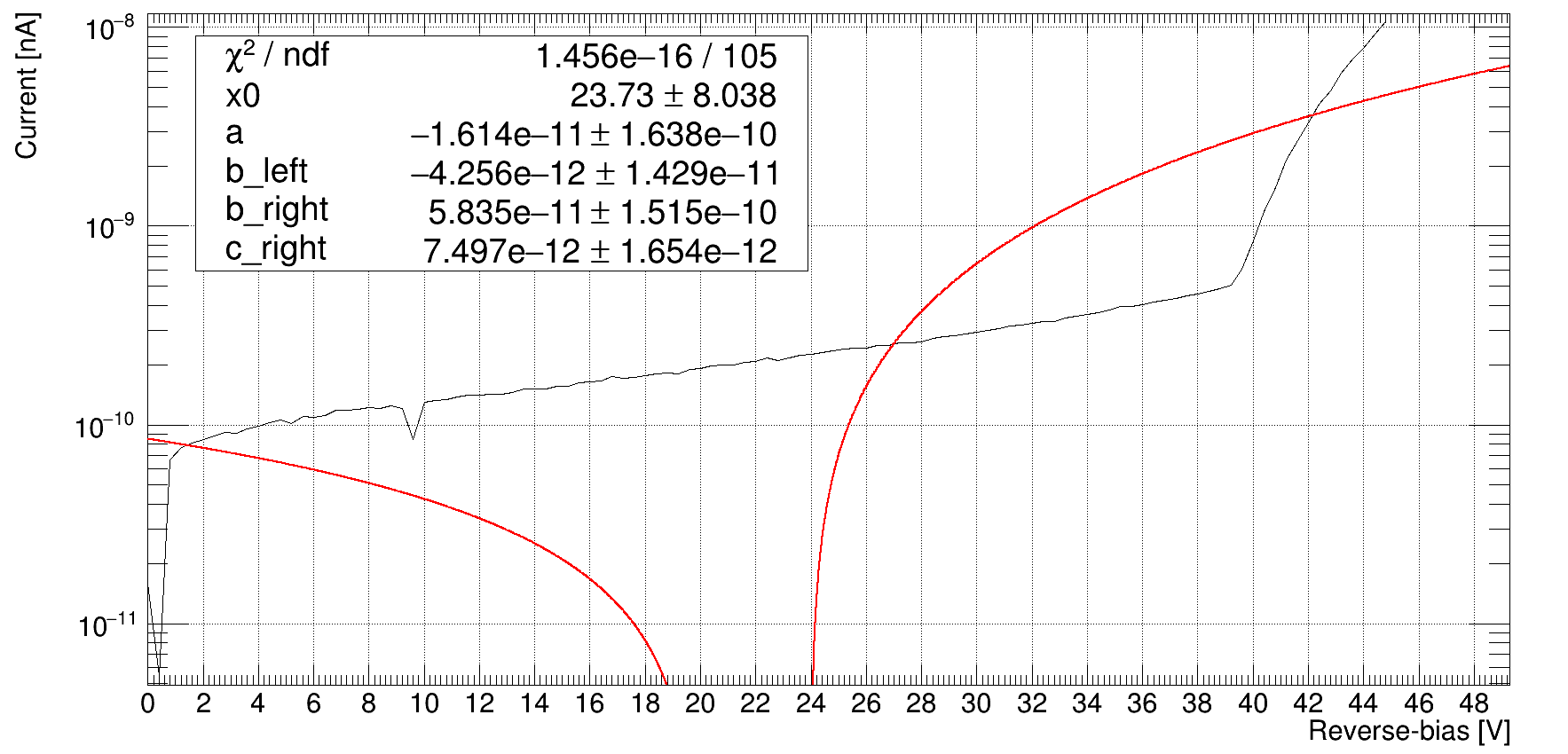
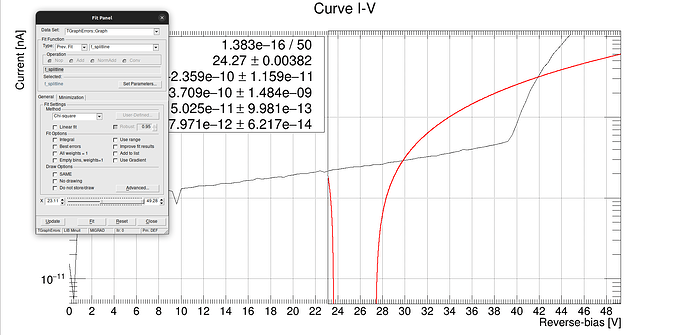
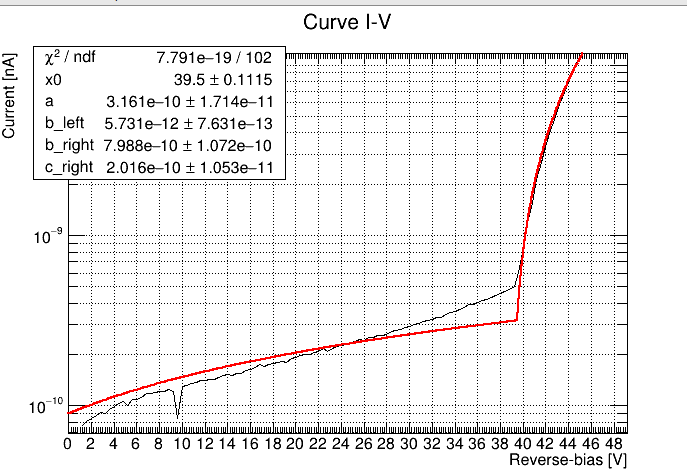
but not the same for another kind of IV curve like Ch1_inv.txt (3,2 KB):
Someone can help me please?