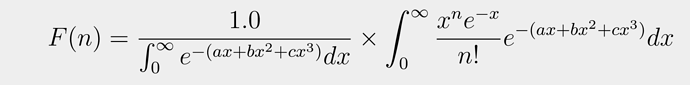Fitting in ROOT with a function having two integrals in it

[Rahul]

Hello ROOT experts,

I am trying to test a model with some data. The equation representing the model has the following approximate form for the distribution of c:

Q(a,b,c) = c!*integral(exp(-x)/exp(ax^2+bx^3)) divided by integral(exp(ax^2+bx^3)) 

Where the integrals are from 0 to infinity. I had success in making a fit for a form in the numerator in the model using the logic in this post: https://root-forum.cern.ch/t/fitting-an-integral-function/8517/8

Trying to make the code for my current purpose with this in mind, I wrote the following fit function

Double_t FitFunction(Double_t *x, Double_t *p)
{
     
    TF2 *main = new TF2("main","[0]*TMath::Factorial(x[0]))*(exp(-y)/exp([1]*pow(y,2)+[2]*pow(y,3)))");  
    main->SetParameters(p[0],p[1],p[2],p[3]);
    TF12 *f12A = new TF12("f12A",main,x[0],"y");
    Double_t mainsum = f12A->Integral(0.0,TMath::Infinity());

    TF2 *deno = new TF2("deno","exp([1]*pow(y,2)+[2]*pow(y,3))" ); 
    main->SetParameters(p[1],p[2],p[3]);
    TF12 *f12B = new TF12("f12B",deno,x[0],"y");
    Double_t part = f12B->Integral(0.0,TMath::Infinity());

    delete main; delete deno;
    delete f12A; delete  f12B; 

    return mainsum/deno;
}

which I will use to fit with the following lines of code

    TF1 *MyFit=new TF1("MyFit",FitFunction,30,40,4);
    MyFit->SetParameter(0,1.0);
    MyFit->SetParameter(1,1.0);
    MyFit->SetParameter(2,1.0);
    MyFit->SetParameter(3,1.0);  
    MyFit->SetParNames("N","#alpha","#beta","#gamma");
    MyFit->SetLineColor(1);
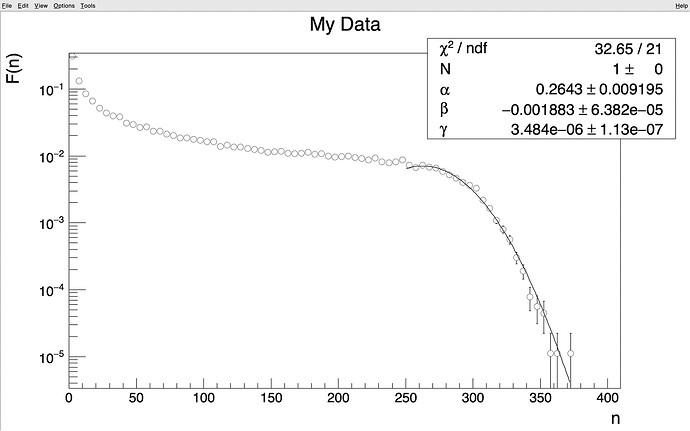
    gr->Fit(MyFit,"RME");//gr is the TGraphErrors instance with the c distribution.

Is this line of thought correct? I am however getting errors like this when I try to perform the fit:

Warning in <ROOT::Math::ROOT::Math::GausIntegrator>: Failed to reach the desired tolerance ; maxtol = 1e-12

I am not yet sure of the possible success of the model but would be grateful to get some suggestions and comments on the way in which I am trying to implement it with ROOT from its experts.

Thank you and regards
Rahul

[moneta]

Hi,
The code seems correct. Maybe the error is sue to the fact you are using an integral in an interval going up to infinity. In that case it is better, for more control, to use instead of TF1::Integral the ROOT::Math::IntegratorOneDim class and the method IntegralUp(..).

Lorenzo

[Rahul]

Hi,

It looks that the limit indeed is the problem. When I change the limits from 0 -> inf to 0 -> a where a < 10.0, the tolerance related error is not coming although the fit is failed.

When I tried to implement ROOT::Math::IntegratorOneDim , I realised that it requires wrapping the function and declaring an integrator (Please correct me if I am wrong).

However, I am not sure how to do that with the form of the function I am having right now (I know how to do it with a TF1 without the complication of parameters for fitting) Especially Wrapping the TF2 *main function and its projection TF12 *f12A at x[0] remembering the fact that the parameters p[1], p[2], p[3] should be there for the TF1 *part function as well. There were some minor mistakes in the earlier version of the code which I corrected now and paste below.

Double_t FitFunction(Double_t *x, Double_t *p)
{
     
    TF2 *main = new TF2("main","[0]*TMath::Factorial(x))*(exp(-y)/exp([1]*pow(y,2)+[2]*pow(y,3)))");  
    main->SetParameters(p[0],p[1],p[2],p[3]);
    TF12 *f12A = new TF12("f12A",main,x[0],"y");
    Double_t mainsum = f12A->Integral(0.0,TMath::Infinity());

    TF2 *part = new TF2("deno","exp([1]*pow(y,2)+[2]*pow(y,3))" ); 
    part->SetParameters(p[1],p[2],p[3]);
    Double_t deno = part->Integral(0.0,TMath::Infinity());

    delete main; delete part;
    delete f12A; 

    return mainsum/deno;
}

Could you please suggest to me how to proceed in this scenario?

Regards
Rahul

[moneta]

Here is a possible solution, note I use a class to avoid creating/deleting object inside the function called in fitting.

struct FitFunction { 

 TF2 * main;
 TF2 * part;
 TF12 * f12A;
 ROOT::Math::IntegratorOneDim ig; 

 FitFunction() { 
  main = new TF2("main","[0]*TMath::Factorial(x))*(exp(-y)/exp([1]*pow(y,2)+[2]*pow(y,3)))");  
   f12A = new TF12("f12A",main,0.,"y");
// it seems to me deno is a function of only one variable
 part = new TF1("deno","exp([1]*pow(x,2)+[2]*pow(x,3))" ); 
 
 ig = new ROOT::Math::IntegratorOneDim(ROOT::Math::IntegrationOneDim::kAdaptiveSingular);
}

double operator() (double *x, double *p) {
   main->SetParameters(p[0],p[1],p[2],p[3]);
   f12A->SetXY(x[0]);
 
   ig->SetFunction(*f12A);
   double mainsum =  ig->IntegralUp(0.);

   part->SetParameters(p[1],p[2],p[3]);
   ig->SetFunction(*part);
   double deno = ig->IntegralUp(0.);
    
   return mainsum/deno;
}

~FitFunction() { 
   delete main; delete part;
    delete f12A; 
   delete ig;
}
};

[Rahul]

Thank you very much for the reply and code.

1. Could you please confirm whether in this case, the fitting should be done in the following fashion or not? :

FitFunction* ff = new FitFunction();
TF1 *MyFit = new TF1("MyFit",ff,&FitFunction::operator(), x_min, x_max, 2);
.... //(x_min, x_max) is the range of fit on the distribution.
....
TGraphErrors* grM = new TGraphErrors(11,binX,binY,binXerr,binYerr);
grM->Fit(MyFit,"RME");

2. Also, I was thinking that when this → f12A = new TF12("f12A",main,0.,"y"); is done, a projection of main at x =0. is made and stored to f12A. Could you please tell me whether the kind of fitting above replace it as a projection of main at x = x[0] which is the value of taken from the x-axis of the distribution owing to this line f12A->SetXY(x[0]);?

[moneta]

Hi,

1. If the function object implements the operator(), it is simpler (see ROOT: TF1 Class Reference).

FitFunction ff;
TF1 *MyFit = new TF1("MyFit",ff, x_min, x_max, 2);

2. Correct. calling f12A->SetXY(x) evaluates the projection at the given passed value in SetXY function.

Lorenzo

[Rahul]

Hi,

Thanks for the confirmation of those two points. When I do the fitting like this

  FitFunction ff ; 
  TF1 * MyFit = new TF1("MyFit",ff, 270, 340, 4);

I get the following error:

root [0] .L Test.C+g
Info in <TMacOSXSystem::ACLiC>: creating shared library /Users/rahul/Desktop/./Test_C.so
root [1] Test()

 *** Break *** segmentation violation
[/usr/lib/system/libsystem_platform.dylib] _sigtramp (no debug info)
[<unknown binary>] (no debug info)
[/Users/rahul/Desktop/Test_C.so] FitFunction::~FitFunction() (no debug info)
[/Users/rahul/Desktop/Test_C.so] TF1::TF1<FitFunction>(char const*, FitFunction, double, double, int, int, TF1::EAddToList) (no debug info)
[/Users/rahul/Desktop/Test_C.so] Test() (no debug info)
[<unknown binary>] (no debug info)
[/Users/rahul/rootbuild/lib/libCling.so] cling::IncrementalExecutor::executeWrapper(llvm::StringRef, cling::Value*) const (no debug info)
[/Users/rahul/rootbuild/lib/libCling.so] cling::Interpreter::RunFunction(clang::FunctionDecl const*, cling::Value*) (no debug info)
[/Users/rahul/rootbuild/lib/libCling.so] cling::Interpreter::EvaluateInternal(std::__1::basic_string<char, std::__1::char_traits<char>, std::__1::allocator<char> > const&, cling::CompilationOptions, cling::Value*, cling::Transaction**, unsigned long) (no debug info)
[/Users/rahul/rootbuild/lib/libCling.so] cling::Interpreter::process(std::__1::basic_string<char, std::__1::char_traits<char>, std::__1::allocator<char> > const&, cling::Value*, cling::Transaction**, bool) (no debug info)
[/Users/rahul/rootbuild/lib/libCling.so] cling::MetaProcessor::process(llvm::StringRef, cling::Interpreter::CompilationResult&, cling::Value*, bool) (no debug info)
[/Users/rahul/rootbuild/lib/libCling.so] HandleInterpreterException(cling::MetaProcessor*, char const*, cling::Interpreter::CompilationResult&, cling::Value*) /Users/rahul/rootbuild/root-6.18.04/core/metacling/src/TCling.cxx:2161
[/Users/rahul/rootbuild/lib/libCling.so] TCling::ProcessLine(char const*, TInterpreter::EErrorCode*) /Users/rahul/rootbuild/root-6.18.04/core/metacling/src/TCling.cxx:0
[/Users/rahul/rootbuild/lib/libRint.so] TRint::ProcessLineNr(char const*, char const*, int*) /Users/rahul/rootbuild/root-6.18.04/core/rint/src/TRint.cxx:746
[/Users/rahul/rootbuild/lib/libRint.so] TRint::HandleTermInput() /Users/rahul/rootbuild/root-6.18.04/core/rint/src/TRint.cxx:608
[/Users/rahul/rootbuild/lib/libCore.so] TUnixSystem::CheckDescriptors() /Users/rahul/rootbuild/root-6.18.04/core/unix/src/TUnixSystem.cxx:1311
[/Users/rahul/rootbuild/lib/libCore.so] TMacOSXSystem::DispatchOneEvent(bool) /Users/rahul/rootbuild/root-6.18.04/core/macosx/src/TMacOSXSystem.mm:378
[/Users/rahul/rootbuild/lib/libCore.so] TSystem::InnerLoop() /Users/rahul/rootbuild/root-6.18.04/core/base/src/TSystem.cxx:413
[/Users/rahul/rootbuild/lib/libCore.so] TSystem::Run() /Users/rahul/rootbuild/root-6.18.04/core/base/src/TSystem.cxx:363
[/Users/rahul/rootbuild/lib/libCore.so] TApplication::Run(bool) /Users/rahul/rootbuild/root-6.18.04/core/base/src/TApplication.cxx:1179
[/Users/rahul/rootbuild/lib/libRint.so] TRint::Run(bool) /Users/rahul/rootbuild/root-6.18.04/core/rint/src/TRint.cxx:463
[/Users/rahul/rootbuild/bin/root.exe] main /Users/rahul/rootbuild/root-6.18.04/main/src/rmain.cxx:32
[/usr/lib/system/libdyld.dylib] start (no debug info)
Root >

And when I do the fitting like this:

  FitFunction* ff = new FitFunction() ; 
  TF1 * MyFit = new TF1("MyFit",ff, &FitFunction::operator(), 270, 340, 4);

the fit fails with the warning:

Warning in <ROOT::Math::ROOT::Math::GausIntegrator>: Failed to reach the desired tolerance ; maxtol = 1e-09

I tried to do this ig -> SetRelTolerance(0.001); as well. But the outcome remained the same with maxtol = 0.001 in the previous warning. I am trying to fit a range in the particular distribution where I am sure from publications that the particular model does work. So I am still confused as to what is going wrong.

Regards
Rahul

[Wile_E_Coyote]

This should work (with no segmentation violation):

FitFunction *ff = new FitFunction();
TF1 *MyFit = new TF1("MyFit", *ff, 270., 340., 4);

[Rahul]

Hi,

There is still a segmentation violation with the code below:

FitFunction *ff = new FitFunction();
TF1 *MyFit = new TF1("MyFit", *ff, 270., 340., 4);

However with this:

FitFunction *ff = new FitFunction();
TF1 *MyFit = new TF1("MyFit", ff, 270., 340., 4);

There is no segmentation violation, but the fit fails with the following warning:

Warning in <ROOT::Math::ROOT::Math::GausIntegrator>: Failed to reach the desired tolerance ; maxtol = 1e-09

Also, when I change the limit of the two integrals like this: ig -> Integral(0.,1.0);, the above warning is not coming although the fit fails with the following log:

 FCN=3574.01 FROM MINOS     STATUS=PROBLEMS       14 CALLS         245 TOTAL
                     EDM=0    STRATEGY= 1  ERROR MATRIX UNCERTAINTY 100.0 per cent
  EXT PARAMETER                APPROXIMATE        STEP         FIRST   
  NO.   NAME      VALUE            ERROR          SIZE      DERIVATIVE 
   1  N            5.00000e+08   6.25605e+08   6.27085e+08   0.00000e+00
   2  #alpha       5.50000e-01   6.72247e-01   6.72247e-01   0.00000e+00
   3  #beta        0.00000e+00   1.49388e+00   1.49388e+00   0.00000e+00
   4  #gamma       0.00000e+00   1.49388e+00   1.49388e+00   0.00000e+00

Regards
Rahul

[moneta]

Hi,
I realised I have posted before a wrong version of the code, for defining the fitting function with the integral, here below is the correct one, which should not give the segmentation violation.
However the functions mathematical definitions look to me not correct, for example they diverge and this certainly explains why the integral does not work. You should check that you have implemented the various functions correctly.
For example : TF2 *part = new TF2("deno","exp([1]*pow(y,2)+[2]*pow(y,3))" ); is a 1D or a 2D function ?
You compute an integral up to + infinity but it diverges.
Then are you sure you want to use TMath::Factorial(x)) ? Is x an integer or a real value ? If it is a real you should use TMath::Gamma(x+1).

Cheers

Lorenzo

TestFitFunction.C (1.2 KB)

[Rahul]

Hi,

Thanks a lot for the code and information.

1. The TF2 *part in your reply is supposed to be a 1D function. It was a mistake which was already corrected.

2. The data points were double. I did not remember about the TMath::Gamma(). So I was converting them into integers. But now I have changed it. Thank you!

3. it looks that the divergence for the integral is coming from the factorial itself as you rightly predicted. I tried to draw this function with the fit values from the publication. It divergences for n > 70, for my case. But in the paper, they have a fit for n as big as 350.

4. Either my understanding of the paper is wrong or something is missing from my code. The exact equation I was trying to calculate is this:

5. The code I currently use for the purpose is this:

#include "TBaseClass.h"

#include "TCanvas.h"

#include "TFile.h"

#include "TObject.h"

#include "TString.h"

#include "TF1.h"

#include "TMath.h"

#include "TStyle.h"

#include "TChain.h"

#include "TF2.h"

#include "TF12.h"

#include "TH1D.h"

#include "TList.h"

#include "TLegend.h"

#include "TLine.h"

#include <cmath>

#include "TGraphAsymmErrors.h"

#include "Math/Integrator.h"

#include <memory>


struct FitFunction {

   std::shared_ptr<TF2> main;
   std::shared_ptr<TF1> part;
   std::shared_ptr<TF12> f12A;
   std::shared_ptr<ROOT::Math::IntegratorOneDim> ig; 

  FitFunction() {
    main = std::make_shared<TF2>("main","[0]*(pow(y,x)*exp(-y)/TMath::Gamma(x+1))/exp(([1]*pow(y,1))+([2]*pow(y,2))+ ([3]*pow(y,3)))");
    f12A = std::make_shared<TF12>("f12A",main.get(),0,"y");
    part = std::make_shared<TF1>("part", "1.0/exp(([0]*pow(x,1))+([1]*pow(x,2))+ ([2]*pow(x,3)))");
    ig   = std::make_shared<ROOT::Math::IntegratorOneDim>(ROOT::Math::IntegrationOneDim::kADAPTIVESINGULAR);
  }

  double operator()(double * x, double * p) {
      main -> SetParameters(p[0], p[1], p[2], p[3]);
      f12A -> SetXY(x[0]); 
      ig -> SetFunction( * f12A);
      double mainsum = ig -> IntegralUp(0.0);

      part -> SetParameters(p[1],p[2],p[3]);
      ig -> SetFunction( * part);
      double deno = ig -> IntegralUp(0.0);

      return mainsum / deno;
    }
};

void TestCode() {

  gStyle -> SetOptStat(1);
  gStyle -> SetOptFit(1);

  TCanvas * canvas = new TCanvas("graph", "Graph");
  canvas -> SetLogy(); 
  //Data
  TFile * File = TFile::Open("DataFile.root");
  if (!File) printf("File Not Found"); 
  TGraphAsymmErrors * gr = dynamic_cast < TGraphAsymmErrors * > (File -> Get("MyData"));
  gr -> Draw("ap"); 

  FitFunction* ff = new FitFunction() ;
  //My Fit
  TF1 * MyFit = new TF1("MyFit",ff, 0,70, 4);
  MyFit ->FixParameter(0, 1.0);
  MyFit ->FixParameter(1, 1.620*pow(10,-1));
  MyFit ->FixParameter(2, -1.35*pow(10,-3));
  MyFit ->FixParameter(3, 2.589*pow(10,-6));

  MyFit -> SetParNames("N", "#alpha", "#beta", "#gamma");
  MyFit -> SetLineColor(1);
  MyFit->Draw("l");
  //gr -> Fit(MyFit, "RME+");

}

6. The data to be fitted (in the range n = 250-350) is attached as a root file below:
   DataFile.root (5.6 KB)
   It was published in Phys.Rev.Lett.87:112303,2001. The fit values are taken from this paper: Nonlinear Dynamics and Applications. Vol. 13 (2006) 282 - 286

7. I was thinking that the TF1 part function of the current version of the code has parameters [0], [1], [2] which must be corresponding to the [1], [2], [3] of TF2 main and setting these parameters incorrectly or writing that in the equation definition incorrectly was the reason. But it now looks that the factorial indeed is causing the trouble. Or else, my understanding of the papers is wrong somewhere.

Could you please have a look that the current version of the code and tell me if there is some obvious mistake in it?

Regards
Rahul

[smgrig]

Hi,
your code is correct in general, but the “main” function can not be integrated in the ROOT at large n (n=250-350). However, it can be integrated if using the Stirling’s approximation for the Gamma function (which is very accurate at n>200). Also, the IntegralUp(0) should be replaced by Integral(0,b) with b>=400.
See the attached code
TestCodeMod.C (2.6 KB)

[Rahul]

Hi,

Great!! Thank you very much for the valuable information you have shared. With the version of the code @smgrig shared, I managed to do the fitting up to n(max) = 372 although I got a few times the warning below:

Warning in <ROOT::Math::ROOT::Math::GausIntegrator>: Failed to reach the desired tolerance ; maxtol = 1e-09

My observation is that the larger the value of n(max), the larger the number of times this warning appears. For n(max) = 372, I got the following fit result.

FCN=32.6498 FROM MINOS     STATUS=SUCCESSFUL    241 CALLS        1110 TOTAL
                     EDM=5.7233e-09    STRATEGY= 1      ERROR MATRIX ACCURATE 
  EXT PARAMETER                                   STEP         FIRST   
  NO.   NAME      VALUE            ERROR          SIZE      DERIVATIVE 
   1  N            1.00000e+00     fixed    
   2  #alpha       2.64313e-01   9.19461e-03  -2.19813e-06  -9.71331e-01
   3  #beta       -1.88310e-03   6.38161e-05   8.99625e-09  -2.66095e+02
   4  #gamma       3.48389e-06   1.13027e-07   1.13027e-07  -4.07085e+04

For visual satisfaction, I am sharing the fit curve below:

Thanks a lot to @moneta, @Wile_E_Coyote and @smgrig for following this topic and kindly leading it up to a reasonable solution with your knowledge.

Regards
Rahul