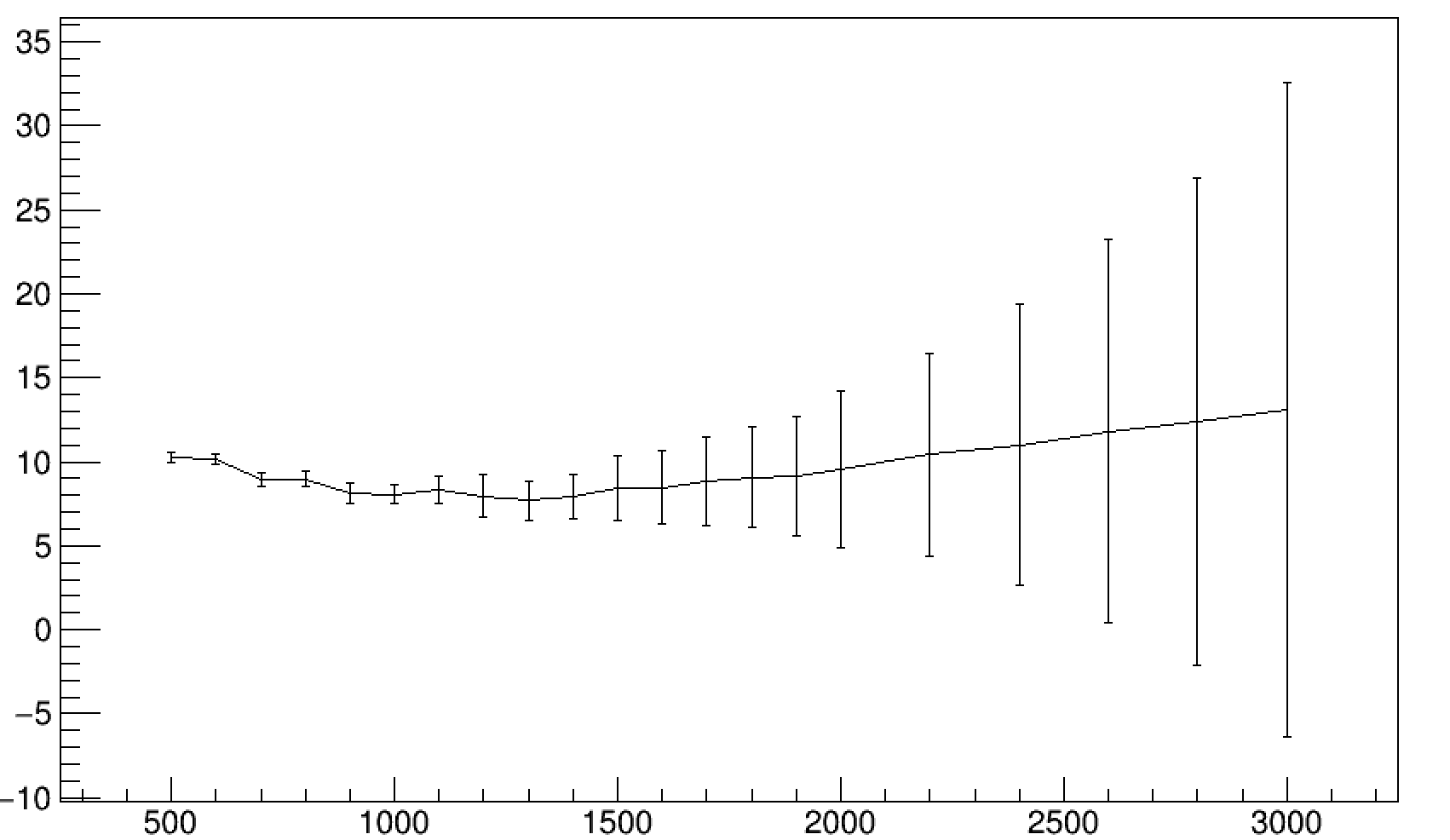Hello,
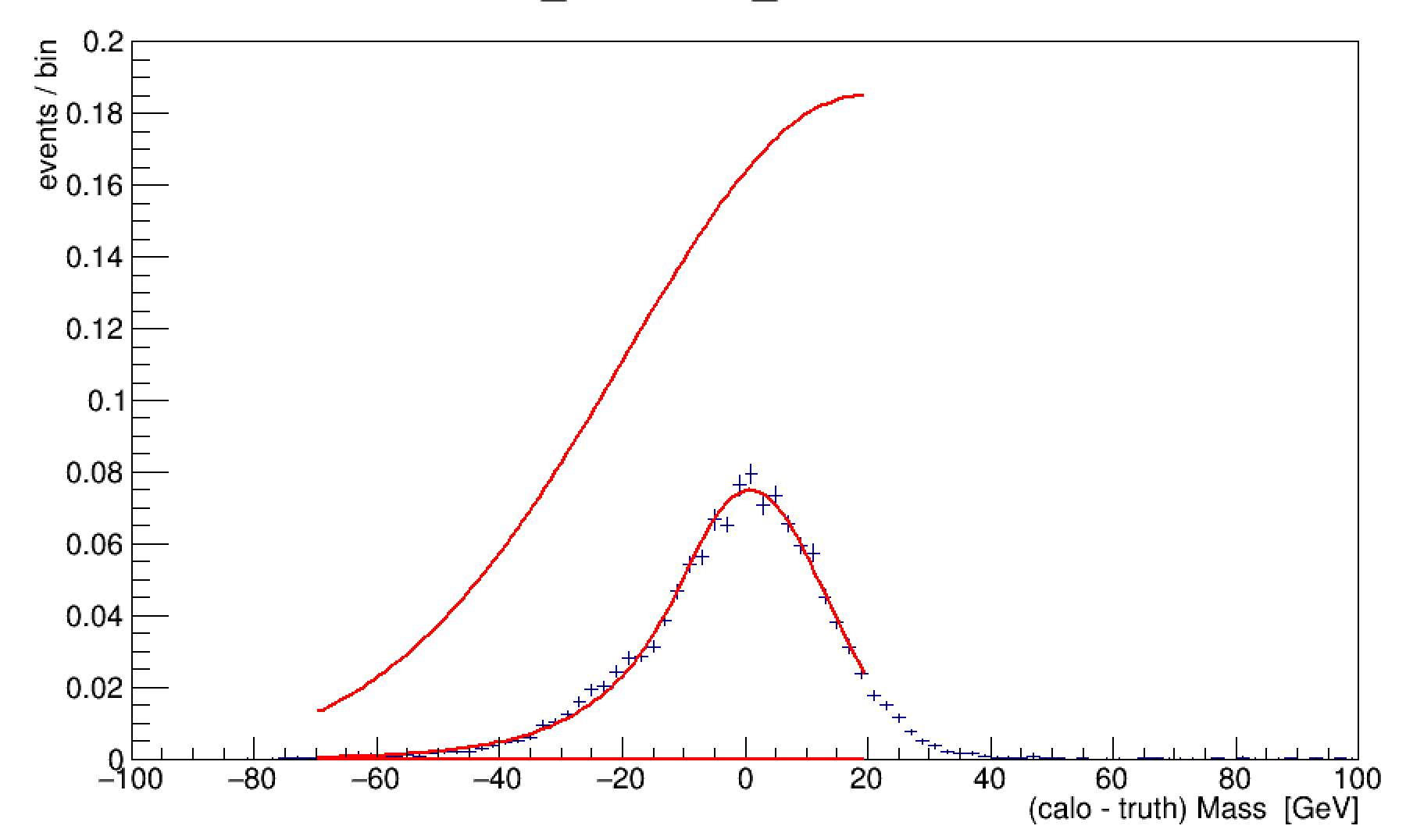
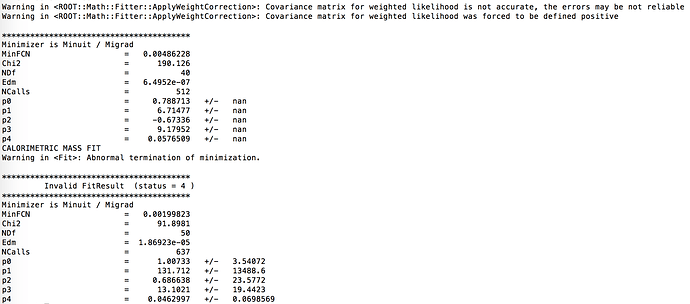
I am trying to fit a set of TH1’s with an user defined function. While the fitted parameters values converge and look very good at first sight, the parameter errors are unnaturally large, as much as 10^2 times the parameter value. I attach with one of such fitted histograms, together with the fitted function plotted with the fit parameters shifter up and down by 1sigma.
Each TH1 is filled as it follows:
[code]
calMtruth_histos.push_back(new TH1F(“h_calM-truth_mass”+mass_name,“h_calM-truth_mass”+mass_name+";(calo - truth) Mass [GeV];events / bin",100,-100,100));
calMtruth_histos.at(i_file)->Sumw2();
calMtruth_histos.at(i_file)->Fill(FatJet_M-V_mass_t,evtWeight*luminosity);
[/code]
The fitting function is a user-defined crystalBall:
double CrystalBall(double* x, double* par){ //http://en.wikipedia.org/wiki/Crystal_Ball_function
double xcur = x[0];
double alpha = par[0];
double n = par[1];
double mu = par[2];
double sigma = par[3];
double N = par[4];
TF1* exp = new TF1("exp","exp(x)",1e-20,1e20); double A; double B;
if (alpha < 0){
A = pow((n/(-1*alpha)),n)*exp->Eval((-1)*alpha*alpha/2);
B = n/(-1*alpha) + alpha;
}
else {
A = pow((n/alpha),n)*exp->Eval((-1)*alpha*alpha/2);
B = n/alpha - alpha;
}
double f;
if ((xcur-mu)/sigma > (-1)*alpha)
f = N*exp->Eval((-1)*(xcur-mu)*(xcur-mu)/ (2*sigma*sigma));
else
f = N*A*pow((B- (xcur-mu)/sigma),(-1*n));
delete exp;
return f;
}The fit is performed with in the following way:
TF1* cball_cal = new TF1("cball2",CrystalBall,-80,80,5);
cball_cal->SetParameter(0,1);
cball_cal->SetParameter(2,calMtruth_histos.at(i_file)->GetMean());
cball_cal->SetParameter(3,calMtruth_histos.at(i_file)->GetRMS()/2);
cball_cal->SetParameter(4,calMtruth_histos.at(i_file)->Integral()/(calMtruth_histos.at(i_file)->GetRMS()*TMath::Sqrt(2*3.141592)));
cout << "CALORIMETRIC MASS FIT" << endl;
TFitResultPtr fitCal = calMtruth_histos.at(i_file)->Fit("cball2","P","",-70,20);
TF1* fitC = calMtruth_histos.at(i_file)->GetFunction("cball2");
I’m doing this as a part of a resolution study on a number of signal samples of increasing mass. Each TH1 pertains to a sample with a certain mass and cross section. The number of actual unweighted events is generally consistent between samples. The cross section however, decreases (and thus so do the event weights) as the sample mass increases.
I noticed that the error on the fitted parameters increases in a roughly linear pattern with the sample mass. I attached an example of the fit output for the last few histograms and an example of the way the parameter errors increase at high sample mass.
Thank you for your help!