Dear all,
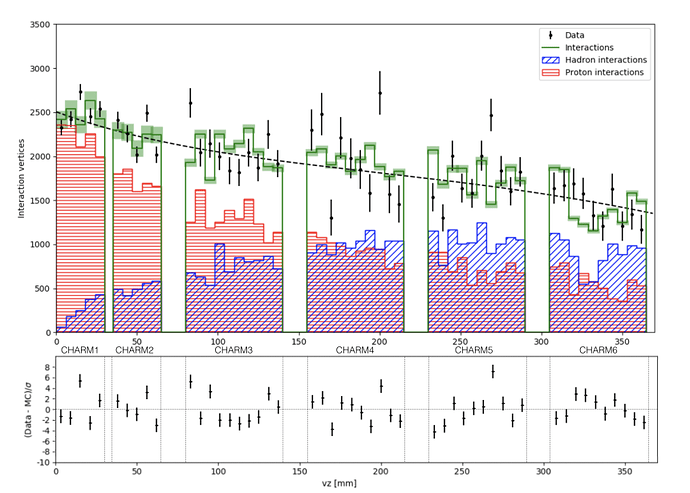
I’m a newbie in root and coding. My purpose is to get data points from an image and using that data create a graph and find the best fitting so that I can get the fit parameters. From the image below I got the points for the dashed line and saved as txt.
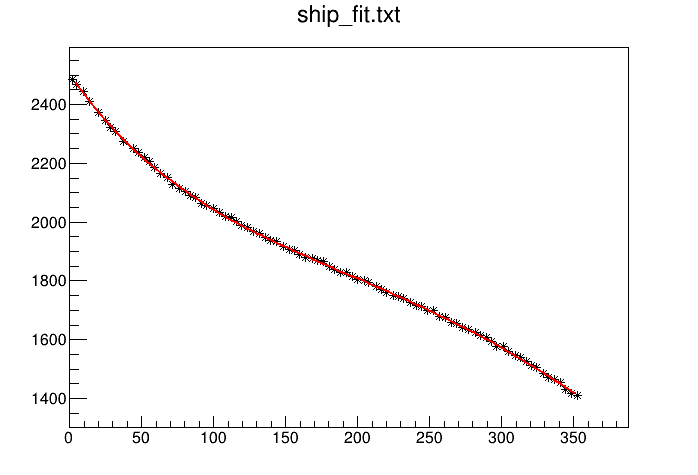
ship_fit.txt (1.4 KB)
The article that I got the image says chi-square fit is performed with an exponential function and 2nd degree polynomial , so that I wrote my macro like this:
void fit()
{
TGraph* gr = new TGraph("ship_fit.txt");
TF1* f = new TF1("f","expo(0)+pol2(2)",0,350);
f->SetParameters(7.37,-0.0074,911.4,4.712,-0.01);
gr->Fit("f","","",1.984,352.729);
gr->Draw("A*");
}
and the result is just like this:
Although it seems okay, chi2/NDf is too big which I guess suggests it is indeed not a good fit. This is the output I get:
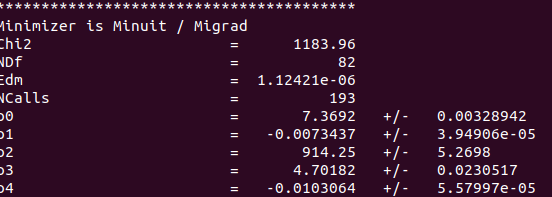
I dont know what I’m doing wrong and why the chi2/NDf is too big although the fit seems okay. Would you help me to clarify? Thank you.
_ROOT Version:5.34/38
Your “data points” have no errors (when fitting, the “x errors” are assumed to be equal to 0, and the “y errors” to 1).
You have 87 (= NDf + 5) “data points”, so the average difference in “y” between your “data points” and your “fitted function” is equal to ±sqrt(1183.96/87) = ±3.69, which seems perfectly fine (see your “fit” plot).
Thank you for your answer, I wasn’t taking sqrt of chi2/ndf . However when I use fit panel I’m getting Invalid Fit Result (status = 4) , when I turn verbose mode, overall output is as just like below. So does it mean minimization can not terminate correctly and then how should I fix this?
root [0] TGraph* g = new TGraph(“ship_fit.txt”)
root [1] g->Draw(“A*”)
Info in TCanvas::MakeDefCanvas: created default TCanvas with name c1
root [2] **********
** 1 **SET PRINT 2
** 2 **SET NOGRAD
PARAMETER DEFINITIONS:
NO. NAME VALUE STEP SIZE LIMITS
1 p0 0.00000e+00 3.00000e-01 no limits
2 p1 0.00000e+00 3.00000e-01 no limits
3 p2 0.00000e+00 3.00000e-01 no limits
4 p3 0.00000e+00 3.00000e-01 no limits
5 p4 0.00000e+00 3.00000e-01 no limits
** 3 **SET ERR 1
** 4 **SET PRINT 2
** 5 **SET STR 1
NOW USING STRATEGY 1: TRY TO BALANCE SPEED AGAINST RELIABILITY
** 6 **MIGRAD 1625 1e-06
FIRST CALL TO USER FUNCTION AT NEW START POINT, WITH IFLAG=4.
START MIGRAD MINIMIZATION. STRATEGY 1. CONVERGENCE WHEN EDM .LT. 1.00e-09
FCN=1.82374e+08 FROM MIGRAD STATUS=INITIATE 49 CALLS 50 TOTAL
EDM= unknown STRATEGY= 1 NO ERROR MATRIX
EXT PARAMETER CURRENT GUESS STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 8.10000e+00 3.00000e-01 8.10000e+00 8.14814e+08
2 p1 0.00000e+00 3.00000e-01 0.00000e+00 1.62306e+11
3 p2 0.00000e+00 3.00000e-01 0.00000e+00 2.47327e+05
4 p3 0.00000e+00 3.00000e-01 0.00000e+00 4.92629e+07
5 p4 0.00000e+00 3.00000e-01 0.00000e+00 1.22224e+10
NO ERROR MATRIX
FCN=6.6221e+06 FROM MIGRAD STATUS=PROGRESS 67 CALLS 68 TOTAL
EDM=3.41736e+07 STRATEGY= 1 NO ERROR MATRIX
EXT PARAMETER CURRENT GUESS STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 8.01410e+00 3.00000e-01 -8.59013e-02 -2.39692e+07
2 p1 -3.83066e-04 3.00000e-01 -3.83066e-04 -1.68216e+10
3 p2 -4.05100e+02 3.00000e-01 -4.05100e+02 -1.02072e+04
4 p3 -1.89330e+00 3.00000e-01 -1.89330e+00 -6.35072e+06
5 p4 -6.21065e-03 3.00000e-01 -6.21065e-03 -2.18257e+09
FCN=63368.3 FROM MIGRAD STATUS=PROGRESS 200 CALLS 201 TOTAL
EDM=81.1391 STRATEGY= 1 ERROR MATRIX UNCERTAINTY 6.3 per cent
EXT PARAMETER APPROXIMATE STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 7.98837e+00 5.03144e-05 2.56069e-04 3.03468e+05
2 p1 -7.28667e-04 6.52657e-06 -1.11234e-04 7.78984e+07
3 p2 -5.31248e+02 2.20519e-01 -8.50486e-01 1.23775e+02
4 p3 -1.53611e+00 1.99516e-02 3.28634e-01 3.10579e+04
5 p4 2.08796e-03 1.63635e-05 -1.84238e-04 8.34372e+06
FCN=57369.6 FROM MIGRAD STATUS=PROGRESS 342 CALLS 343 TOTAL
EDM=1468.83 STRATEGY= 1 ERROR MATRIX UNCERTAINTY 15.7 per cent
EXT PARAMETER APPROXIMATE STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 7.99431e+00 8.53472e-05 6.42341e-04 1.47449e+05
2 p1 -1.73336e-03 8.90680e-06 -1.00798e-04 5.11789e+07
3 p2 -5.39303e+02 2.14311e-01 -1.48669e+00 8.85159e+01
4 p3 1.21397e+00 2.33492e-02 2.82874e-01 3.02666e+04
5 p4 -2.34805e-04 2.41496e-05 -3.09155e-04 1.31460e+07
FCN=21328 FROM MIGRAD STATUS=PROGRESS 474 CALLS 475 TOTAL
EDM=3343.95 STRATEGY= 1 ERROR MATRIX UNCERTAINTY 11.1 per cent
EXT PARAMETER APPROXIMATE STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 8.02097e+00 7.58521e-05 6.80431e-03 9.70528e+05
2 p1 -3.83698e-03 3.38398e-06 -4.40070e-04 2.33534e+08
3 p2 -5.91810e+02 2.15193e-01 -1.37955e+01 7.89185e+02
4 p3 6.69291e+00 8.60528e-03 1.09999e+00 1.90615e+05
5 p4 -8.92055e-03 1.73308e-05 -1.98362e-03 5.13023e+07
FCN=1303.34 FROM MIGRAD STATUS=PROGRESS 597 CALLS 598 TOTAL
EDM=1.08156e-05 STRATEGY= 1 ERROR MATRIX UNCERTAINTY 3.5 per cent
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 8.05091e+00 2.16122e-04 1.94880e-08 2.30286e+02
2 p1 -5.26738e-03 9.13202e-06 3.10959e-09 1.15099e+04
3 p2 -6.39873e+02 3.87669e-01 1.44423e-03 8.46470e-03
4 p3 9.84147e+00 1.94133e-02 -2.20464e-05 7.03673e+00
5 p4 -1.53865e-02 4.27405e-05 5.66499e-08 1.81168e+03
FCN=1290.69 FROM MIGRAD STATUS=PROGRESS 734 CALLS 735 TOTAL
EDM=1.5006 STRATEGY= 1 ERROR MATRIX UNCERTAINTY 24.5 per cent
EXT PARAMETER APPROXIMATE STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 8.00181e+00 7.65704e-03 -4.29815e-03 2.61136e+04
2 p1 -5.38550e-03 1.78054e-05 -1.03648e-05 2.19973e+06
3 p2 -4.89228e+02 2.31055e+01 1.29138e+01 1.49438e+01
4 p3 9.38957e+00 7.66083e-02 -3.90729e-02 1.81643e+03
5 p4 -1.49728e-02 8.38692e-05 3.63597e-05 3.55833e+05
FCN=1276.2 FROM MIGRAD STATUS=PROGRESS 868 CALLS 869 TOTAL
EDM=1.52755 STRATEGY= 1 ERROR MATRIX UNCERTAINTY 24.2 per cent
EXT PARAMETER APPROXIMATE STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 7.94724e+00 7.56070e-03 -3.97633e-03 2.04141e+04
2 p1 -5.52331e-03 1.94878e-05 -7.19893e-06 2.94503e+06
3 p2 -3.30557e+02 2.15132e+01 1.14018e+01 1.78164e+01
4 p3 8.91031e+00 6.80798e-02 -4.10811e-02 3.34591e+03
5 p4 -1.45353e-02 6.98067e-05 4.70146e-05 7.81027e+05
FCN=1264.69 FROM MIGRAD STATUS=PROGRESS 1001 CALLS 1002 TOTAL
EDM=4.62412 STRATEGY= 1 ERROR MATRIX UNCERTAINTY 19.5 per cent
EXT PARAMETER APPROXIMATE STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 7.90053e+00 9.47704e-03 -7.04114e-03 2.43576e+04
2 p1 -5.64496e-03 2.43488e-05 -1.96046e-05 2.88143e+06
3 p2 -2.01288e+02 2.57988e+01 1.92786e+01 1.85802e+01
4 p3 8.51188e+00 8.34001e-02 -5.85793e-02 2.61859e+03
5 p4 -1.41668e-02 8.53749e-05 5.38409e-05 4.49265e+05
FCN=1252.84 FROM MIGRAD STATUS=PROGRESS 1135 CALLS 1136 TOTAL
EDM=0.907471 STRATEGY= 1 ERROR MATRIX UNCERTAINTY 26.3 per cent
EXT PARAMETER APPROXIMATE STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 7.85685e+00 7.03586e-03 5.85962e-04 4.03151e+03
2 p1 -5.76241e-03 1.86240e-05 -8.76122e-07 8.01438e+05
3 p2 -8.58385e+01 1.82404e+01 -1.55093e+00 3.82964e+00
4 p3 8.14939e+00 6.28863e-02 9.22939e-03 5.00921e+02
5 p4 -1.38242e-02 7.18052e-05 -1.62822e-05 2.12869e+04
FCN=1242.09 FROM MIGRAD STATUS=PROGRESS 1262 CALLS 1263 TOTAL
EDM=2.25251 STRATEGY= 1 ERROR MATRIX UNCERTAINTY 22.9 per cent
EXT PARAMETER APPROXIMATE STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 7.81068e+00 7.82250e-03 -7.17154e-04 6.01977e+03
2 p1 -5.89380e-03 2.41946e-05 -3.58670e-06 -4.03069e+05
3 p2 3.13223e+01 1.95059e+01 1.75910e+00 -3.53569e-01
4 p3 7.77728e+00 6.35191e-02 -3.93091e-03 -9.29328e+02
5 p4 -1.34687e-02 6.74873e-05 7.59085e-07 -2.42949e+05
FCN=1231.5 FROM MIGRAD STATUS=PROGRESS 1395 CALLS 1396 TOTAL
EDM=1.46972 STRATEGY= 1 ERROR MATRIX UNCERTAINTY 23.1 per cent
EXT PARAMETER APPROXIMATE STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 7.76230e+00 7.89836e-03 -2.00566e-03 5.52125e+03
2 p1 -6.03027e-03 2.46527e-05 -2.07816e-06 -1.16786e+05
3 p2 1.48018e+02 1.87627e+01 4.58306e+00 1.44571e+00
4 p3 7.39579e+00 6.36993e-02 -2.08984e-02 -2.16427e+02
5 p4 -1.30946e-02 7.09136e-05 2.91804e-05 -1.39942e+04
FCN=1220.47 FROM MIGRAD STATUS=PROGRESS 1533 CALLS 1534 TOTAL
EDM=1.09439 STRATEGY= 1 ERROR MATRIX UNCERTAINTY 30.7 per cent
EXT PARAMETER APPROXIMATE STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 7.70686e+00 8.34018e-03 -8.95449e-03 1.38209e+04
2 p1 -6.19528e-03 2.39349e-05 -2.78253e-05 1.34166e+06
3 p2 2.75053e+02 1.87333e+01 2.01674e+01 1.29569e+01
4 p3 6.97808e+00 6.65895e-02 -6.66933e-02 1.91070e+03
5 p4 -1.26882e-02 7.43855e-05 6.64515e-05 4.10921e+05
CALL LIMIT EXCEEDED IN MIGRAD.
MIGRAD TERMINATED WITHOUT CONVERGENCE.
FCN=1214.44 FROM MIGRAD STATUS=CALL LIMIT 1626 CALLS 1627 TOTAL
EDM=2.02219 STRATEGY= 1 ERROR MATRIX UNCERTAINTY 85.1 per cent
EXT PARAMETER APPROXIMATE STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 7.67523e+00 1.22072e-02 -8.00786e-03 8.66575e+03
2 p1 -6.29576e-03 3.95563e-05 -2.66411e-05 1.09900e+06
3 p2 3.44503e+02 2.65671e+01 1.74915e+01 1.10303e+01
4 p3 6.74894e+00 8.95211e-02 -5.69387e-02 2.17729e+03
5 p4 -1.24655e-02 9.20188e-05 5.45460e-05 5.42702e+05
EXTERNAL ERROR MATRIX. NDIM= 25 NPAR= 5 ERR DEF=1
1.490e-04 4.714e-07 -3.243e-01 1.085e-03 -1.075e-06
4.714e-07 1.565e-09 -1.027e-03 3.348e-06 -3.193e-09
-3.243e-01 -1.027e-03 7.058e+02 -2.361e+00 2.339e-03
1.085e-03 3.348e-06 -2.361e+00 8.014e-03 -8.110e-06
-1.075e-06 -3.193e-09 2.339e-03 -8.110e-06 8.467e-09
ERR MATRIX APPROXIMATE
PARAMETER CORRELATION COEFFICIENTS
NO. GLOBAL 1 2 3 4 5
1 0.99997 1.000 0.976 -1.000 0.993 -0.957
2 0.99977 0.976 1.000 -0.977 0.945 -0.877
3 0.99999 -1.000 -0.977 1.000 -0.993 0.957
4 0.99999 0.993 0.945 -0.993 1.000 -0.985
5 0.99986 -0.957 -0.877 0.957 -0.985 1.000
ERR MATRIX APPROXIMATE
Info in TMinuitMinimizer::Minimize: Finished to run MIGRAD - status 4
Warning in : Abnormal termination of minimization.
Invalid FitResult (status = 4 )
Minimizer is Minuit / Migrad
Chi2 = 1214.44
NDf = 82
Edm = 2.02219
NCalls = 1627
p0 = 7.67523 +/- 0.0469784
p1 = -0.00629576 +/- 0.000152229
p2 = 344.503 +/- 102.241
p3 = 6.74894 +/- 0.344513
p4 = -0.0124655 +/- 0.000354126
In ROOT, before you try to fit your graph or histogram, you MUST set “reasonable” initial values for ALL parameters of your function (except for some “built-in” formulas, like “expo”, 1-D and 2-D “landau”, 1-D and 2-D “gaus”, “chebyshev”, “pol”, for which the standard fit procedure can automatically “guess” them). Otherwise, the fitting procedure may easily misbehave.
The functions that I use are expo and pol2 which are built-in formulas however, does adding them cause the error in the case of guessing parameters? If so how can I set reasonable initial values? I’m sorry for asking too much but although I checked tutorials, I couldn’t understand how they came up with parameter initilization.
ROOT can “automatically” compute initial values of parameters for simple predefined formulas like “expo”, 1-D and 2-D “landau”, 1-D and 2-D “gaus”, “chebyshev”, “pol”. As soon as you need a more complicated function, you need to set them yourself.
In your first post here, you used:
f->SetParameters(7.37, -0.0074, 911.4, 4.712, -0.01);
In the “Fit Panel”, you need to use the “SetParameters...” button.
Actually the parameters I use in my first post were the rounded results of the fit that I did by using Fit Panel. I think I figure out the reason for Invalid FitResult (status = 4 ). In order to see what would happen if I define the functions myself and not SetParameters I wrote this macro
#include "TMath.h"
Double_t quadratic(Double_t *x, Double_t *par)
{
return par[0] + par[1]*x[0] + par[2]*x[0]*x[0]; // pol2
}
Double_t exponential(Double_t *x, Double_t *par)
{
return par[0]*TMath::Exp(-x[0]*par[1]); // expo
}
Double_t combine(Double_t *x, Double_t *par)
{
return quadratic(x,par)+ exponential(x,&par[3]);
}
void combining()
{
TGraph* gr = new TGraph("ship_fit.txt");
gr->GetXaxis()->SetTitle("vz(mm)");
gr->GetYaxis()->SetTitle("Interaction Vertices");
gr->Draw("A*");
TF1 *fit = new TF1("fit",combine,0,350,5);
fit->SetParNames("A","B","C","Constant","Lambda");
gr->Fit("fit");
}
Then again it gave me the error Invalid FitResult (status = 4 ). Then I changed the last line of my code in order to fit only in a limited region:
gr->Fit("fit","","",1,344);
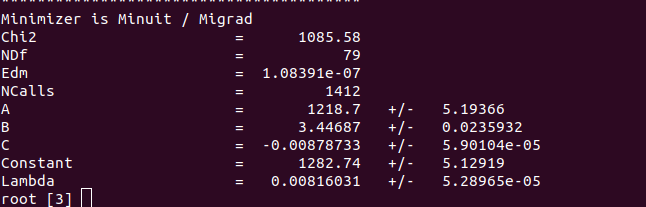
Now, there is no Invalid FitResult (status = 4 ) and also sqrt(chi2/ndf) becomes 0.42. So excluding the last 3 data points fixed the issue I guess but what is the reason behind? and how was ROOT able to guess the parameters although the function I define is more complicated one since it is an addition of two functions?
In your case, a very simple "pol5" formula gives very good results.
BTW. “sqrt(Chi2/NDf)” is meaningless (you want "sqrt(Chi2/(NDf+number_of_free_parameters))" as “NDf+number_of_free_parameters” = number of used “data points”).