Fitting a Linear Function

Newbie
1

Hi All,
I’m a ROOT newbie and trying to fit a simple linear function but the values of parameters and chi^2/ndf are not coming nice. What am I missing?

I’ve uploaded the cpp file, data file and graph png below.

Thanks.

test.cpp (328 Bytes)
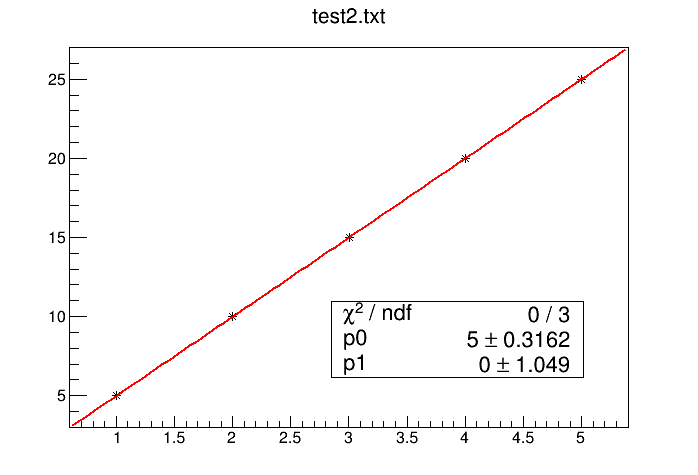
test2.txt (25 Bytes)

c1
c1698×475 4.41 KB

Please read tips for efficient and successful posting and posting code

ROOT Version: Not Provided
Platform: Not Provided
Compiler: Not Provided

1 Like
2

Everything is perfectly fine.

1 Like
3

Thanks for replying @Wile_E_Coyote I understand why chi^2 is zero but isn’t the ratio chi^2/ndf must be equals to 1 for a good fit. In other words, what’s the significance of this ratio, does it has to be 1 every time?

Also If I slightly change the initial parameters : f1->SetParameters(3,3)

the values of p0, p1 and chi^2 comes out to be drastically different. Can you please explain it?

Thanks.

1 Like
4

For how to “interpret” chi^2 (and chi^2 / NDF) you need to look into some statistics book.

I don’t get any problem if I set initial parameters (3,3). For me, it returns Chi2=2.3e-22 (“almost” 0), p0=5±2.8e-12 and p1=3e-12±9.2e-12 (“almost” 0).

1 Like
5

Ok! Here I knew the slope and intercept beforehand but in cases where I don’t, how would I know that the parameter values are “almost” correct? Should I have to completely rely on chi^2/NDF ratio?

6

You always get “parameter” ± “parameter_error” (i.e. you never get any “true” / “real” / “undisputed” / “absolute” values).

1 Like
7

Ok! Thanks @Wile_E_Coyote for your help!

8

In ROOT, before you try to fit your graph or histogram, you MUST set “reasonable” initial values for ALL parameters of your function (except for some “built-in” formulas, like “gaus”, for which the standard fit procedure can automatically “guess” them), otherwise the fitting procedure may easily misbehave.

Search for “Setting initial conditions” in the TGraph::Fit and TH1::Fit methods descriptions.

2 Likes