Hi Wile and Lorenzo
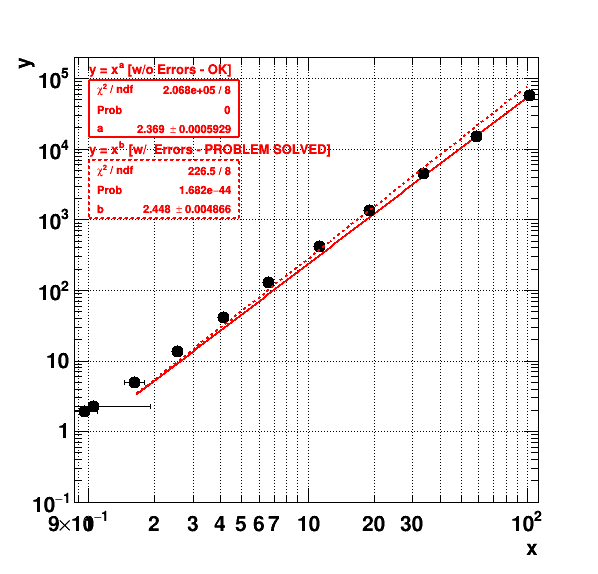
Thanks for your suggestions and comments. The brutal fix suggested by Wile works for me:
However it is interesting also going more in depth (since I am quite ignorant in this matter), since I might learn from this experience. To let you understand what exactly I am doing, I wrote a bit more information here below:
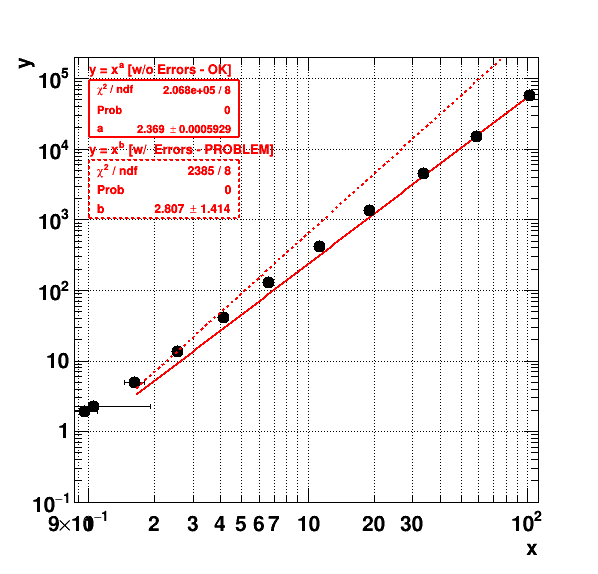
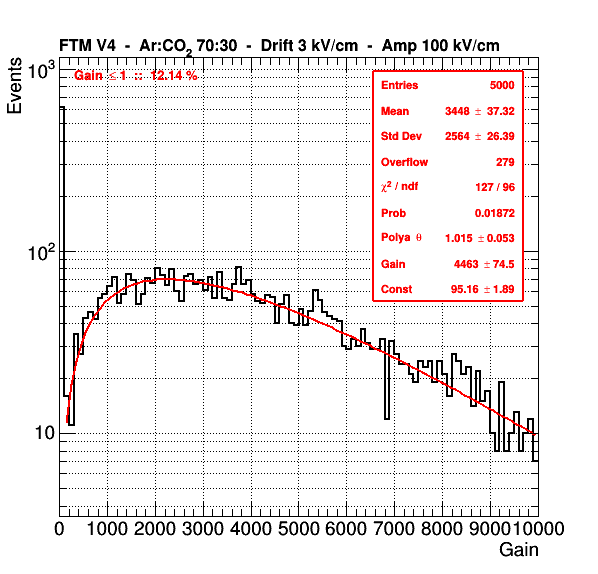
I am performing simulations of electron avalanches in gaseous detectors, with Garfield, which exhibit quite large fluctuations. I (and also other people [1]) believe that the fluctuations in the final avalanche are determined by the fluctuations in the first part of the avalanche [2]. We believe that N_{full} = N_{half}^a, with a \approx 2. Therefore I am making a plot here of the full avalanche gain on the y-axis vs the simulation of a only half of the avalanche on the x-axis. The gain (or average avalanche statistics) is obtained through a Polya fit [3]. If I take a data point with the smallest uncertainty: the second before last point:
x (simulation of 1/2 avalanche): Gain = 33.6369 +/- 0.378424 Rel Err = 1.12503 % (First plot below)
y (simulation of full avalanche): Gain = 4463.23 +/- 74.5165 Rel Err = 1.66956 % (Second plot below)
I would believe the fits are of good quality (What exactly is this “Probability” that gets plotted in the Statbox?) so I would assume that the uncertainty I assigned to the values is a reasonable uncertainty. On the other hand I do not expect that my model N_{full} = N_{half}^a, with a \approx 2 describes this data with incredible precision, since it is just a rough model…
Although the simulations are done independently, I would say that the x and y values are correlated, but for the uncertainty on the x and y-values I am not able to say so. I use the same function to fit and to extract the uncertainty for the x- and y-values, so maybe the uncertainties are correlated and I should use a 2d likelihood fit as you propose? In case you have some RooFit example / tutorial in mind, I ll be happy to try it.
Thanks a lot
Kind regards
Piet
[1] T. Zerguerras et al. NIM A 772, (2015) 76. https://doi.org/10.1016/j.nima.2014.11.014
[2] For instance if due to fluctuations half way the simulation of the avalanche, you have a very small amount of electrons, then it is unlikely that this will be corrected in the second part of the avalanche, and very likely you wlll end up with a small charge, because each of the electrons created in the first part of the avalanche can be considered as starting points for another avalanche in the second half of the total avalanche. And therefore fluctuations on a large number will result in a more averaged number.
[3] P(N_{e}) = \frac{(1+\theta)^{1+\theta}}{\Gamma(1+\theta)} \left( \frac{N_{e}}{G} \right)^\theta \exp \left[ -(1+\theta)\frac{N_{e}}{G} \right], where G = Gain = average of N_e and \theta is the Polya parameter related to the relative gain variance f = \frac{1}{1+\theta}. Just checking now I see it belongs to the group of Negative Binomial Distributions. See also: http://mathworld.wolfram.com/NegativeBinomialDistribution.html