Fit does not include all values

Newbie
1

I have not learned anything about programming but was told how to write a specific program and to add my own data. In an experiment on the IV characteristics of an LED I have drawn a graph and need to fit the equation y=η0.026ln(x/I+1)+R*x. η should be around 2 and I ideally of an order between 10^-9 and ^-15. R is an unknown

My x(Id) and y(Vd) values are as follows:
|Id = (6e-08 ± 5.03e-08)A, | Vd = (0.0609 ± 0.0005609)V|
|Id = (7e-08 ± 5.035e-08)A, | Vd = (0.1718 ± 0.0006718)V|
|Id = (9e-08 ± 5.045e-08)A, | Vd = (0.2805 ± 0.0007805)V|
|Id = (1e-07 ± 5.05e-08)A, | Vd = (0.3791 ± 0.0008791)V|
|Id = (1.1e-07 ± 5.055e-08)A, | Vd = (0.4789 ± 0.0009789)V|
|Id = (1.6e-07 ± 5.08e-08)A, | Vd = (0.969 ± 0.001469)V|
|Id = (8e-06 ± 5.04e-06)A, | Vd = (1.448 ± 0.001948)V|
|Id = (0.000254 ± 6.27e-06)A, | Vd = (1.6 ± 0.0021)V|
|Id = (0.000661 ± 8.305e-06)A, | Vd = (1.643 ± 0.002143)V|
|Id = (0.00101 ± 5.505e-05)A, | Vd = (1.662 ± 0.002162)V|
|Id = (0.00134 ± 5.67e-05)A, | Vd = (1.68 ± 0.00218)V|
|Id = (0.001807 ± 5.9035e-05)A, | Vd = (1.694 ± 0.002194)V|
|Id = (0.00218 ± 6.09e-05)A, | Vd = (1.705 ± 0.002205)V|
|Id = (0.0026 ± 6.3e-05)A, | Vd = (1.715 ± 0.002215)V|
|Id = (0.00304 ± 6.52e-05)A, | Vd = (1.726 ± 0.002226)V|
|Id = (0.00342 ± 6.71e-05)A, | Vd = (1.733 ± 0.002233)V|
|Id = (0.003798 ± 6.899e-05)A, | Vd = (1.74 ± 0.00224)V|
|Id = (0.00423 ± 7.115e-05)A, | Vd = (1.748 ± 0.002248)V|
|Id = (0.00464 ± 7.32e-05)A, | Vd = (1.754 ± 0.002254)V|
|Id = (0.00502 ± 7.51e-05)A, | Vd = (1.76 ± 0.00226)V|
|Id = (0.00539 ± 7.695e-05)A, | Vd = (1.766 ± 0.002266)V|
|Id = (0.00583 ± 7.915e-05)A, | Vd = (1.773 ± 0.002273)V|
|Id = (0.00622 ± 8.11e-05)A, | Vd = (1.778 ± 0.002278)V|
|Id = (0.00658 ± 8.29e-05)A, | Vd = (1.783 ± 0.002283)V|
|Id = (0.00703 ± 8.515e-05)A, | Vd = (1.789 ± 0.002289)V|
|Id = (0.00742 ± 8.71e-05)A, | Vd = (1.794 ± 0.002294)V|
|Id = (0.00782 ± 8.91e-05)A, | Vd = (1.799 ± 0.002299)V|
|Id = (0.00826 ± 9.13e-05)A, | Vd = (1.804 ± 0.002304)V|
|Id = (0.00861 ± 9.305e-05)A, | Vd = (1.808 ± 0.002308)V|
|Id = (0.00905 ± 9.525e-05)A, | Vd = (1.813 ± 0.002313)V|
|Id = (0.00941 ± 9.705e-05)A, | Vd = (1.817 ± 0.002317)V|
|Id = (0.00982 ± 9.91e-05)A, | Vd = (1.821 ± 0.002321)V|
|Id = (0.01022 ± 0.0001011)A, | Vd = (1.825 ± 0.002325)V|
|Id = (0.01066 ± 0.0001033)A, | Vd = (1.83 ± 0.00233)V|
|Id = (0.01104 ± 0.0001052)A, | Vd = (1.834 ± 0.002334)V|
|Id = (0.01141 ± 0.00010705)A, | Vd = (1.838 ± 0.002338)V|
|Id = (0.01182 ± 0.0001091)A, | Vd = (1.842 ± 0.002342)V|
|Id = (0.01221 ± 0.00011105)A, | Vd = (1.846 ± 0.002346)V|
|Id = (0.01268 ± 0.0001134)A, | Vd = (1.85 ± 0.00235)V|
|Id = (0.01304 ± 0.0001152)A, | Vd = (1.853 ± 0.002353)V|
|Id = (0.01348 ± 0.0001174)A, | Vd = (1.858 ± 0.002358)V|
|Id = (0.01381 ± 0.00011905)A, | Vd = (1.861 ± 0.002361)V|
|Id = (0.01429 ± 0.00012145)A, | Vd = (1.865 ± 0.002365)V|
|Id = (0.01463 ± 0.00012315)A, | Vd = (1.868 ± 0.002368)V|

I have drawn a TGraphErrors of this data. There is no error message, but the following code gives me the attached graph:

TF1 *f = new TF1("f","[0]*0.026*log((x/[1])+1)+[2]*x",1e-10,0.016);

  f->SetParName(0,"n");
  f->SetParName(1,"Is");
  f->SetParName(2,"Rd");

  f->SetParameter(0,2);
  f->SetParLimits(1,1e-15,1e-9);
  f->SetParLimits(2,0,100);

  f->SetLineColor(4);
  g->Fit(f,"RM+");

c

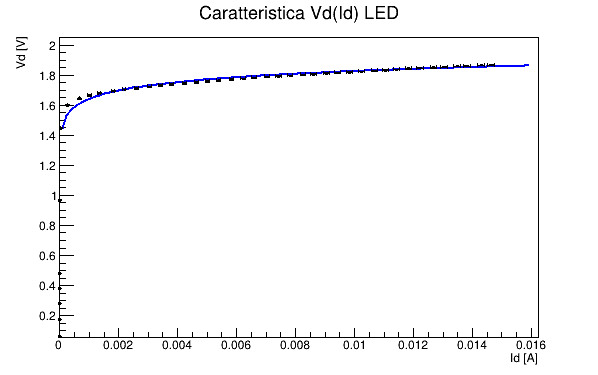
The fit does not include the first values. The parameters it works out are:
FCN=1857.86 FROM HESSE STATUS=OK 20 CALLS 681 TOTAL
EDM=8.68354e-07 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 n 3.00572e+00 2.44840e-02 3.01218e-06 1.18727e-02
2 Is 7.29039e-13 1.27725e-13 6.20209e-07 -2.31475e-01
3 Rd 1.74960e-01 1.52251e-01 9.56173e-06 -4.76620e-02
X2 = 1857.86, number of DOF: 41 (Probability: 0).

The plotted points form the expected shape and the parameter values about, so I don’t understand what I’ve done wrong?

2

It seems to me that your function is not able to describe your data (in the full range) well. Try this:

{
  // Id-Vd characteristic of a LED
  // https://root-forum.cern.ch/t/fit-does-not-include-all-values/33472
  // experimental data in four columns: Id[A] eId[A] Vd[V] eVd[V]
  Double_t IV[][4] = {
    {6e-08, 5.03e-08, 0.0609, 0.0005609},
    {7e-08, 5.035e-08, 0.1718, 0.0006718},
    {9e-08, 5.045e-08, 0.2805, 0.0007805},
    {1e-07, 5.05e-08, 0.3791, 0.0008791},
    {1.1e-07, 5.055e-08, 0.4789, 0.0009789},
    {1.6e-07, 5.08e-08, 0.969, 0.001469},
    {8e-06, 5.04e-06, 1.448, 0.001948},
    {0.000254, 6.27e-06, 1.6, 0.0021},
    {0.000661, 8.305e-06, 1.643, 0.002143},
    {0.00101, 5.505e-05, 1.662, 0.002162},
    {0.00134, 5.67e-05, 1.68, 0.00218},
    {0.001807, 5.9035e-05, 1.694, 0.002194},
    {0.00218, 6.09e-05, 1.705, 0.002205},
    {0.0026, 6.3e-05, 1.715, 0.002215},
    {0.00304, 6.52e-05, 1.726, 0.002226},
    {0.00342, 6.71e-05, 1.733, 0.002233},
    {0.003798, 6.899e-05, 1.74, 0.00224},
    {0.00423, 7.115e-05, 1.748, 0.002248},
    {0.00464, 7.32e-05, 1.754, 0.002254},
    {0.00502, 7.51e-05, 1.76, 0.00226},
    {0.00539, 7.695e-05, 1.766, 0.002266},
    {0.00583, 7.915e-05, 1.773, 0.002273},
    {0.00622, 8.11e-05, 1.778, 0.002278},
    {0.00658, 8.29e-05, 1.783, 0.002283},
    {0.00703, 8.515e-05, 1.789, 0.002289},
    {0.00742, 8.71e-05, 1.794, 0.002294},
    {0.00782, 8.91e-05, 1.799, 0.002299},
    {0.00826, 9.13e-05, 1.804, 0.002304},
    {0.00861, 9.305e-05, 1.808, 0.002308},
    {0.00905, 9.525e-05, 1.813, 0.002313},
    {0.00941, 9.705e-05, 1.817, 0.002317},
    {0.00982, 9.91e-05, 1.821, 0.002321},
    {0.01022, 0.0001011, 1.825, 0.002325},
    {0.01066, 0.0001033, 1.83, 0.00233},
    {0.01104, 0.0001052, 1.834, 0.002334},
    {0.01141, 0.00010705, 1.838, 0.002338},
    {0.01182, 0.0001091, 1.842, 0.002342},
    {0.01221, 0.00011105, 1.846, 0.002346},
    {0.01268, 0.0001134, 1.85, 0.00235},
    {0.01304, 0.0001152, 1.853, 0.002353},
    {0.01348, 0.0001174, 1.858, 0.002358},
    {0.01381, 0.00011905, 1.861, 0.002361},
    {0.01429, 0.00012145, 1.865, 0.002365},
    {0.01463, 0.00012315, 1.868, 0.002368}
  };
  
  UInt_t n = sizeof(IV) / sizeof(IV[0]);
  
  TGraphErrors *g = new TGraphErrors(n);
  g->SetTitle("Vd(Id) characteristic of a LED;Id [A];Vd [V]");
  for (UInt_t i = 0; i < n; i++) {
    g->SetPoint(i, IV[i][0], IV[i][2]);
    g->SetPointError(i, IV[i][1], IV[i][3]);
  }
  g->Sort(); // just a precaution
  // g->Print();
  
  //
  // The realistic, non-ideal Id-Vd characteristic of a p-n junction
  // diode is described by an implicit function in form ("Id" and "Vd"
  // are, respectively, the diode's current and voltage):
  //
  // Id - (Vd - Id * Rs) / Rp = Is * (std::exp((Vd - Id * Rs) / (n * Vth)) - 1.)
  //
  // where "Is" (a scale current), "Rs" (a parasitic series resistance),
  // "Rp" (a parasitic parallel resistance) and "n" (an ideality factor)
  // are the parameters of the function which need to be found by the fit
  // and "Vth = k * T / e = (T [K] / 300. [K]) / 38.681740 [V]" (a thermal
  // voltage) is just a constant.
  //
  // In general, one cannot rewrite the above equation into an explicit
  // function, neither into "Id = f(Vd)" nor into "Vd = f(Id)".
  //
  // However, we can try to fit experimental data with two simplified formulas:
  // 1. for small "Id" and "Vd", we can neglect the term with "Is" and then:
  //    Vd = (Rs + Rp) * Id
  // 2. for big "Id" and "Vd", we can neglect the term with "Rp" and then:
  //    Vd = n * Vth * std::log(Id / Is + 1.) + Rs * Id
  // Hopefully we do not have any intermediate "Id" and "Vd" data points!
  //
  
  TF1 *f = new TF1("f", // Note: x = Id, f(x) = Vd
                   "TMath::Min(([2] + [3]) * x, [0] * [4] * TMath::Log(x / [1] + 1.) + [2] * x)",
                   g->GetXaxis()->GetXmin(), g->GetXaxis()->GetXmax());
  f->SetParNames("n", "Is", "Rs", "Rp", "Vth");
  f->SetNpx(1000);
  f->SetLineColor(4);
  
  // Note: Vth = k * T / e = 1. / 38.681740 V at 300 K
  f->SetParameters(1.5, 5e-20, 5., 5e6, 1. / 38.681740);
  // f->SetParameters(1.7, 4.6e-20, 6.4, 5e6, 1. / 38.681740);
  // f->SetParLimits(0, 1., 2.); // "n"
  // f->SetParLimits(1, 1e-55, 1e-5); // "Is"
  // f->SetParLimits(2, 0., 100.); // "Rs"
  // f->SetParLimits(3, 1e3, 1e9); // "Rp"
  f->FixParameter(4, 1. / 38.681740); // "Vth"
  
  g->Fit(f, ""); // "" or "M" or "EX0 or "W"
  
  // gStyle->SetStatStyle(0); gStyle->SetOptFit(112); // 112 or 1112
  g->Draw("AP");
  f->Draw("SAME L");
  gPad->SetLogx(1);
}