Fit after rebin

ROOT
1

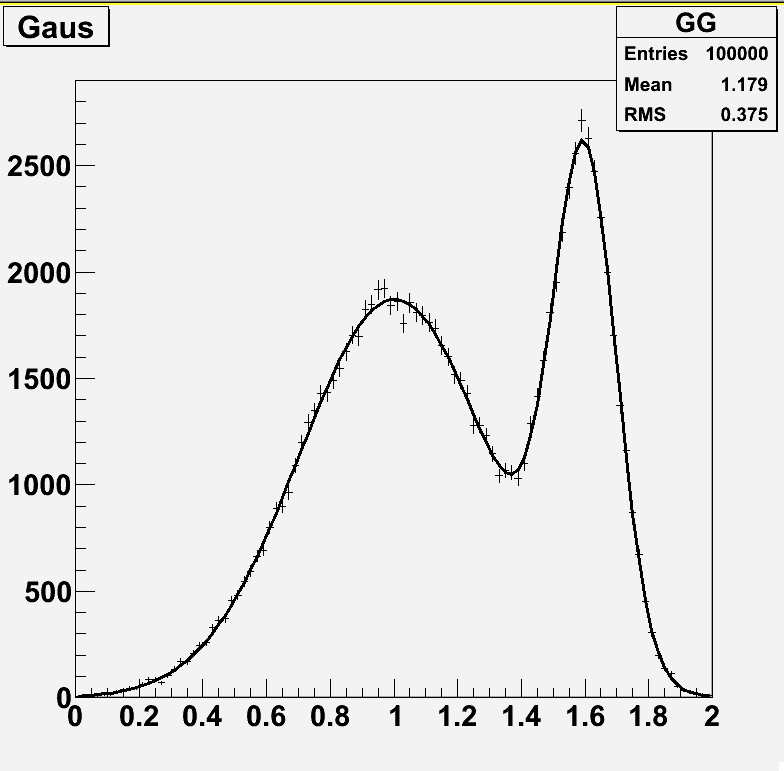
Hi,
can anyone help me to understand why if I:

  • get/create an histo
  • rebin it
  • fit it

the fit converges but with wrong parameters (the normalization is wrong because scaled by the rebinning and the bin width)?
I’m probably missing something so … what’s the best procedure to follow if I need to rebin a histo before to fit it?

Here is my session and an example attached (norm = par[0] is the integral of the function that in this case is also the number of entries in the histo); you can easly see that the histo has 100000 but the fit gives me norm = 2000 (because I’ve merged 2 bins with a width of 0.01 with rebin … it looks like the “algorithm” is norm = entries * mergedBins * binWidth).

Processing TRandomGaus.C…
FCN=90.9116 FROM MIGRAD STATUS=CONVERGED 504 CALLS 505 TOTAL
EDM=3.25234e-11 STRATEGY= 1 ERROR MATRIX UNCERTAINTY 0.6 per cent
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 1.99939e+03 6.32964e+00 -2.70582e-04 1.41782e-06
2 p1 2.97092e-01 2.47305e-03 -1.56102e-07 6.91556e-04
3 p2 1.60052e+00 8.33687e-04 1.03970e-07 -2.72906e-03
4 p3 1.00454e-01 7.29726e-04 -4.46622e-08 -4.68483e-03
5 p4 1.00169e+00 1.91583e-03 7.14263e-08 -3.24564e-03
6 p5 2.99705e-01 1.39516e-03 -1.96906e-08 9.52031e-05

This becomes a problem when I have to fit several histos but using different bin width and/or rebin!
I’d like to get the right number directly from par[0].

Thanks in advance!

P.S.: I’m using ROOT 5.26/00 on Max OS X 10.6.4

Bye…

RandomGaus.png784×771 14.3 KB


TRandomGaus.C (1.84 KB)

2

Hi,

I don’t understand your problem. The fitted function represents the expected number of counts/bin. The integral of the function in x, is not the sum of all the counts/bin, but it is equal to the number of entries multiplied by the in width.
Therefore, if you rebin, I am expecting that your “norm” parameter will change according to the new bin width. If you want it constant just divide your fitting function by the bin width.

Best Regards

Lorenzo