Fit a paraboloid to a TGraph2D

ROOT
1

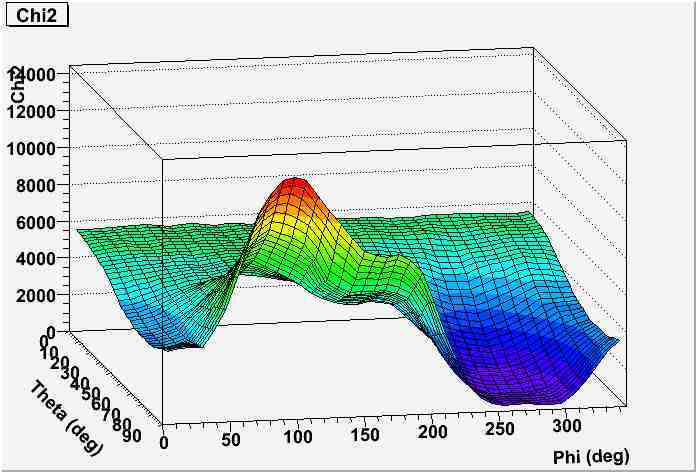
Hi,

I have a TGraph2D which follows a non-standard function. I’d like to fit the area that is around the minimum of this TGraph2D with a paraboloid:

z = (x-x0)^2/a^2 + (y-y0)^2/b^2 +z0

My code looks like:

TGraph2D *g = new TGraph2D(nDataFiles,th,ph,zh);
g->Draw("surf1");

TF2 *paraboloid = new TF2("paraboloid","pow(x-[0],2)/([2]*[2]) + pow(y-[1],2)/([3]*[3] +[4])",xmin-15.,xmin+15.,ymin-60.,ymin+60.);
  paraboloid -> SetParameters(45.,180.,1.,1.,100.);
  paraboloid -> SetParNames("x0","y0","a","b","offset");
  gStyle -> SetOptFit(1111);	//To add fit parameters to plot legend
  g-> Fit("paraboloid","RMLL");
   paraboloid->Draw("same");

The problem is that the fit is totally “unstable”. It only converges when I initialize z0=1, and in this case it gives completely wrong values from the fit for z0. When I put z0=100 (that is actually quite close to the value it actually has), the fit does not converge at all.

Is is possible to set somehow the tolerance of the fit, or do something to make it more stable?

Any hint of what could be the reason that the whole fit procedure is so sensible to the initial parameters?

I guessed that not having enough

Thanks,
Estela.

2

Hi,

I will have to see your graph to understand why is not so stable.
In general, your definition of parameter is not the optimal one for fitting.
I would use the fact that the paraboloid is a linear function of the parameters and eventually use the linear fitter, which does not require initial parameter values.
So, I would define your function as

TF2 *paraboloid = new TF2("paraboloid","[0]*x*x++[1]*x++[2]*y*y++[3]*y++[4]",xmin-15.,xmin+15.,ymin-60.,ymin+60.);

Note the usage of “++” to indicate that the function is linear and the linear fitter can be used.

Best Regards

Lorenzo

3

Hi,

I send attached how the function looks like. I am trying to fit around the minimum, that is at around (75,270,100)

I tried as well with the equation of the paraboloid as you suggested:

TF2 *parabol = new TF2("parabol","[0]*x*x++[1]*x++[2]*y*y++[3]*y++[4]",xmin-15.,xmin+15.,ymin-60.,ymin+60.);
That is what I get:

Error in <TDecompChol::Decompose()>: matrix not positive definite Error in <TDecompChol::Solve()>: Decomposition failed Error in <TLinearFitter::Eval>: Matrix inversion failed Fitting results: Parameters: NO. VALUE ERROR 0 0.000000e+00 0.000000e+00 1 0.000000e+00 0.000000e+00 2 0.000000e+00 0.000000e+00 3 0.000000e+00 0.000000e+00 4 0.000000e+00 0.000000e+00 Chi2(parabol fit) = 0

When using my method, with initial parameters

TF2 *paraboloid = new TF2("paraboloid","pow(x-[0],2)/([2]*[2]) + pow(y-[1],2)/([3]*[3] +[4])",xmin-30.,xmin+30.,ymin-60.,ymin+60.); paraboloid -> SetParameters(45.,180.,1.,1.,100.);

I get:

FCN=901145 FROM MIGRAD STATUS=CONVERGED 1195 CALLS 1196 TOTAL EDM=2.98925e-09 STRATEGY= 1 ERROR MATRIX UNCERTAINTY 2.0 per cent EXT PARAMETER STEP FIRST NO. NAME VALUE ERROR SIZE DERIVATIVE 1 x0 8.09188e+01 8.32839e-03 -1.66440e-05 -1.18550e-03 2 y0 2.71348e+02 4.60644e-03 6.74196e-06 -7.50910e-04 3 a 8.18694e-01 4.14682e-04 -4.78098e-07 2.61238e-01 4 b 9.31235e+00 8.84350e-04 -1.19790e-07 3.05383e+00 5 z0 -8.52562e+01 1.66506e-02 2.54928e-06 1.62728e-01
At least in this case it gives something, but the value of z0 is completely wrong.

Thanks for your help,
Estela.

c1.jpg696×472 32.9 KB

4

Hi,
but what is the error on z0 ? The correct re-scaled eror you get from

parabol->GetParError(4);

The fact that the linear fitter fails is an indication that the data are not really modeling correctly your function. You might need to set a smaller fit range.
If you need more help, you would need to send me a root file with your graph2D object.
Regards

Lorenzo