Fisher distribution diverging where it shouldn't

Newbie
1

Please read tips for efficient and successful posting and posting code

ROOT Version: 5.34
Platform: Ubuntu Virtual Machine on Windows10 host
Compiler: CINT/ROOT C/C++ Interpreter version 5.18.00

Hello, I’m trying to implement an F-test to compare two fit models, but my function seems diverging somewhere when the degrees of freedom of my models get too high.

void Ftest(){
  Int_t ndf1=105;
  Int_t ndf2= 102;

  TF1 *pdf= new TF1("pdf","TMath::Gamma(([0]+[1])/2)/(x*TMath::Gamma([0]/2)*TMath::Gamma([1]/2))*TMath::Power([0]*x,[0]/2)*TMath::Power([1],[1]/2)/(TMath::Power([0]*x+[1],([0]+[1])/2))",0,5);
  pdf->SetParameters(ndf1,ndf2);
  pdf->SetTitle("F distribution");

  TCanvas *distr= new TCanvas("distr","F test",1000,800);
  pdf->Draw();
  Double_t probabilita = pdf->Integral(1,5);  

  printf("Probability:%f\n", probabilita);
}

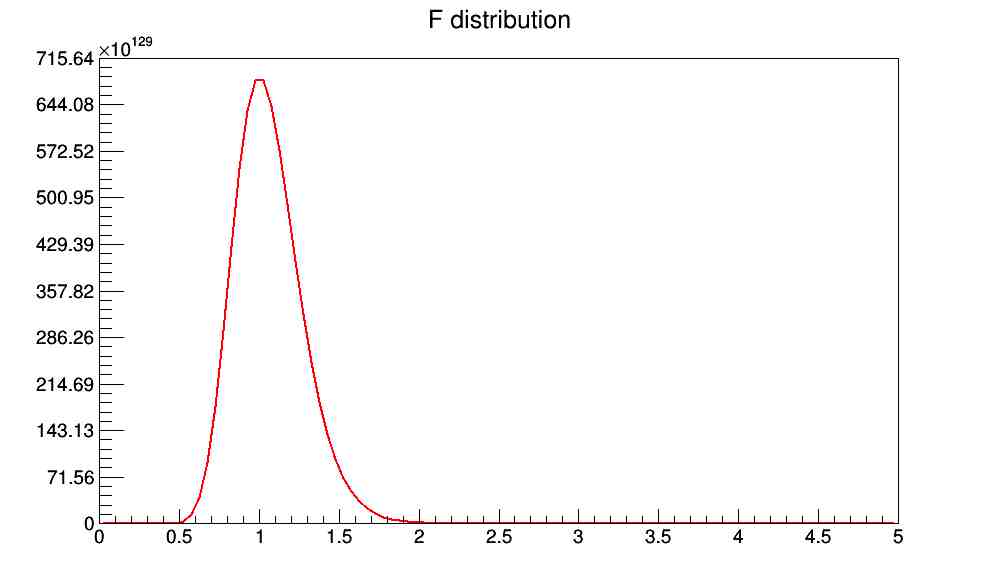
When the two ndf1 and ndf2 are low, the function has the expected shape for a Fisher distribution. When the degrees of freedom are around 100, it has the shape in the figure, but you can see it goes way too high in amplitude and therefore, goes to infinity for higher values (my ndfs should be around 300).

ftest
ftest.jpg998×582 17.7 KB

Is there some problem with the definition of the function?

Ftest.C (475 Bytes)

2

Can it be a normalization problem of the gamma function?

3

Hi,
there is an error in the final part instead of this

/(TMath::Power([0]*x+[1],([0]+[1])/2))
------>
*(TMath::Power([0]*x+[1],-([0]+[1])/2))

or you can use the PDF fdistirbution_pdf() implemented in ROOT, in a macro like this

void macro(){

    TF1 *f= new TF1("f","ROOT::Math::fdistribution_pdf(x,[0],[1])",0,5);
    
    f->SetParameters(105,102);
    f->SetNpx(1e4);
    f->Draw();
}

Below I attached the plot with your formula corrected and the pdf of f-distribution superimposed. They are perfectly superimposed.

Cheers,
Stefano

18
Schermata 2019-11-20 alle 07.54.18.png1944×1640 157 KB

1 Like
4

Thank you, I didn’t even know this function existed :sweat_smile: It makes things so much easier :smiley: