Hi Rene,
Thanks a lot for the reference. As you posted in
root.cern.ch/phpBB2/viewtopic.php?t=1033
Double_t GetX(Double_t y, Double_t xmin = 0, Double_t xmax = 0) const
also seems useful for root finding.
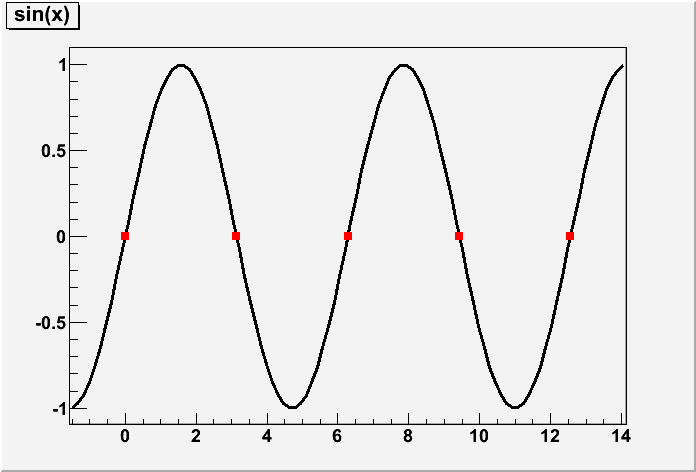
What I cannot fully accomplish is to find all the roots in the
interval. These methods (GetX and GetMinimum) return a single value;
so I tried to use them repeatedly in order to retrieve all the roots.
So I wrote this
#include <iostream>
#include <vector>
void Solve(vector<double>& roots, int nest, TF1* f, double s, double e)
{
double r = f->GetX(0, s, e);
cout << "(" << nest << ") start=" << s << " end=" << e << " root="
<< r << endl;
roots.push_back(r);
if (r != s && r !=e) {
Solve(roots, nest+1, f, s, r);
Solve(roots, nest+1, f, r, e);
}
}
void FindRoot()
{
double s = - TMath::PiOver2();
double e = 2 * TMath::TwoPi() + TMath::PiOver2();
cout << "start =" << s << endl;
cout << "end =" << e << endl;
// Create the function and wrap it
TF1* f = new TF1("Sin Function", "sin(x)", s, e);
f->Draw();
vector<double> roots;
Solve(roots, 0, f, s, e);
sort(roots.begin(), roots.end());
double* xx = new double[roots.size()];
double* yy = new double[roots.size()];
// If this is put here; then only the first point
// is shown in the plot.
//TGraph* gr = new TGraph(7, xx, yy);
cout << "Found " << roots.size() << " roots:";
for (int i = 0; i < roots.size(); ++i) {
xx [i] = roots[i];
yy [i] = 0;
cout << xx[i] << " ";
}
cout << endl;
TGraph* gr = new TGraph(7, xx, yy);
gr->SetMarkerColor(kRed);
gr->SetMarkerStyle(21);
gr->Draw("P");
c1->Update();
cout.flush();
}
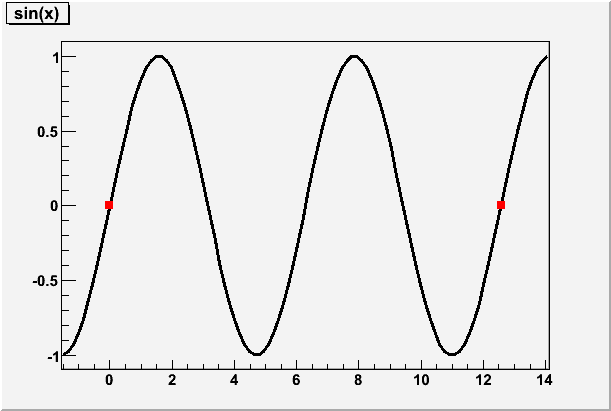
Running it I only get the outer roots in the interval. Cout’s output
for the run is
start =-1.5708
end =14.1372
TCanvas::MakeDefCanvas: created default TCanvas with name c1
(0) start=-1.5708 end=14.1372 root=12.5664
(1) start=-1.5708 end=12.5664 root=-4.50437e-10
(2) start=-1.5708 end=-4.50437e-10 root=-4.50437e-10
(3) start=-1.5708 end=-4.50437e-10 root=-4.50437e-10
(3) start=-4.50437e-10 end=-4.50437e-10 root=-4.50437e-10
(2) start=-4.50437e-10 end=12.5664 root=-4.50437e-10
(1) start=12.5664 end=14.1372 root=12.5664
Found 7 roots:-4.50437e-10 -4.50437e-10 -4.50437e-10 -4.50437e-10
-4.50437e-10 12.5664 12.5664
And the resulting plot is attached (also the same script).
Taking a look in TF1’s docs:
- For GetMinimumX the search interval is specified as “(xmin, xmax)” which seems to denote an open interval.
- For GetX the search interval is specified as “(xmin<x<xmax)” which also signals an open interval.
- In the underlying ROOT::Math::RootFinder, the comments for “SetFunction” talk about “search interval [xlow, xup]” (ie closed interval).
Also note that for TF1::GetMinimun, TF1::GetMinimunX and TF1::GetX the description says “…the grid search is used to bracket the maximum…”. Maybe, at least the first two, should speak about bracketing the minimum.
Thanks a lot for your advice. Cheers.
FindRoot.C (1.2 KB)