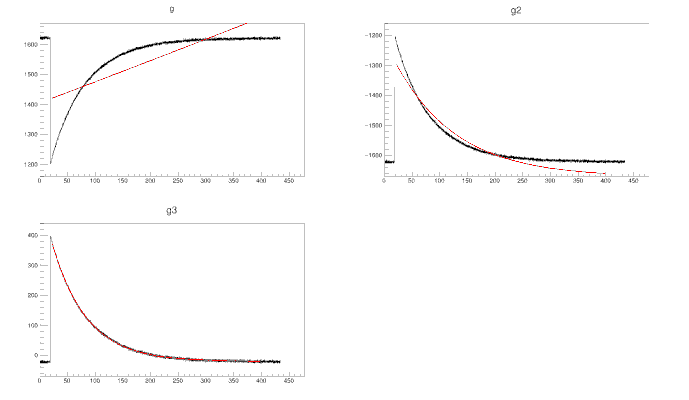
Hello, I try to fit a very basic curve using a function like A+Bexp(Cx). I use ROOT 6.06/00.
I attached the source file (exp.txt) as well as a screenshot of what I get.
The code of the macro that produces this is the following
[code]{
TGraph *g = new TGraph(“exp.txt”);
double *x = g->GetX();
double *y = g->GetY();
TF1 *f = new TF1(“f”,“pol0+expo(1)”,20,400);
TCanvas *c = new TCanvas(“c”,“c”);
c->Divide(2,2);
c->cd(1);
g->Draw();
g->SetTitle(“g”);
g->Fit(f,“RB”);
c->cd(2);
double y2[8192] = {0.};
for(int i=0 ; i<8192 ; i++)
y2[i] = -1.*y[i];
TGraph *g2 = new TGraph(8192,x,y2);
g2->SetTitle(“g2”);
//f->SetParameter(0,1600); //if you uncomment this, it will fit correctly. Please note that it is not “-1600”
g2->Draw();
g2->Fit(f,“RB”);
c->cd(3);
double y3[8192] = {0.};
for(int i=0 ; i<8192 ; i++)
y3[i] = y2[i]+1600;
TGraph *g3 = new TGraph(8192,x,y3);
g3->SetTitle(“g3”);
g3->Draw();
g3->Fit(f,“RB”);
}[/code]
So I have several questions. Maybe some of them are really naive ones about fitting procedure.
1/Why does the fit of g2 fails except if I set pol0 to “1600” (and not “-1600” as expected).
2/ Why do I am not able to fit g directly whatever the parameter value I set? It seems that the fit procedure does not work very well when the B parameter is negative
So basically, is there some specific precaution if I want to fit such curve? Sorry if my questions are not so clear but I wonder why the exponential in some cases and not in other ones.
Thank you in advance.
exp.txt (109 KB)