Hi,
I am attaching a plot that shows a pol3 fit to a histogram. I see that the red. chi2 is quite small but the error on the fit parameters are very large. I am not sure why this is happening.
Also if I fit a pol1 instead to this histogram, I still get a low red. chi2. and the error on the parameters are smaller. Is there a generic way of finding out which polynomial will be a better fit to a given histogram. I thought of red. chi2, but the reduced chi2 in both cases (pol1 and pol3) are quite small.
debdatta,
Take any statistics/data analysis book and look at F-test for
determining the order of the polynomial .
Eddy
HI Eddy,
thanks for your reply. I had another question about the fit. If you see the chi2/ndf, the ndf = 21. I am not sure why is this 21 and not 25 , b.c. there are 25 bins and the fitted function extends over all the 25 bins.
-thanks Debdatta.Hi Debdatta,
You have 25 data points and are fitting 4 parameters (p0,…,p3) .
Therefore, the number of degrees of freedom equals
21 = 25-4
Eddy
Hi Eddy,
thanks again and I am sorry I have another question. Are the diagonal elements of the error/covariance matrix = error on the parameters ?
so if I have three parameters, s.t
float par0 = f1->GetParameter(0);
float par0_err = f1->GetParError(0);
Is errormatrix[0][0] = par0_err ?
I dont see this happening in the examples that I am looking at.
-thanks Debdatta.Hi Debdatta,
The variance in the fit parameter is the diagonal entry in the
covariance matrix so that the error is the sqrt of that number .
However, … some routines might apply a scaling factor where the
justification goes along the following lines :
If you data has errors that are Gaussian distributed , the chisquare/ndf
has an expectation value of one . So if one is not sure
about the exact size of the error in the data points and since the
variance in the fit parameters is linear dependent on them,
one could scale the diagonal entries by chisquare/ndf , so the
error by the sqrt(chisquare/ndf) .
Eddy
ps.
- Typing into google “Bevington F-test” gave the following link
explaining how to apply the F-test to decide on the order of
your polynome:
lise.lbl.gov/chbooth/papers/Hamilton_XAFS13.pdf
- I bet that a “pol1” will do the job .
HI Eddy,
thanks for sending the link to F test. If I am not mistaken, it basically compares the red. chi2 for two different tests.
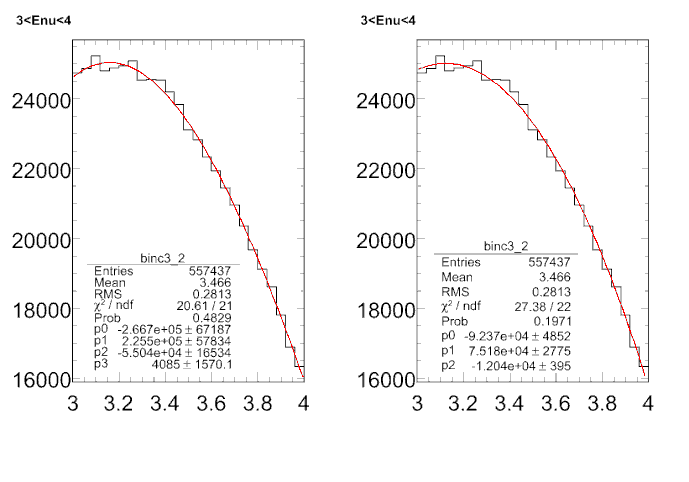
I am attaching a histogram. There are two fits, one pol3(left) and one pol2(right) to the same histogram. This fit is done with the least square method (dflt for polynomial fit).
The pol3 has a smaller reduced chi2 compared to pol2. But the error on the pol3 parameters is much larger than that compared to pol2.
If I do the same fit with the “F” option then it uses the MINUIT option. In this case, the pol3 fit gives me the message : error matrix not positive definite.
This means that there is something going wrong with the pol3 fit.
There is no way of telling this if I look at the red. chi2 alone. Should I look at a combination of the red. chi2 and the parameter errors ?
debdatta,
Both fit results tell you that your problem is ill conditioned . Each
is using a different matrix inversion algorithm where the Minuit one
checks that the matrix is positive definite .
The matrix that your invert in order to get the error matrix is
called a Vandermonde matrix . For higher-order polynomials it
can be ill conditioned .
So what can you do :
-
if you insist on fitting with polynomes, have a look at
solveLinear.C in the tutorials directory . I show there how
to solve a linear fitting problem with some simple linear
algebra . The advantage is that you will have the matrix
before inverting and you can check its condition number
and then know the numerical error in the inversion. -
Switch to using Chebyshev polynomials
Eddy
Hi every one,
I permise me to go on this discussion because I have the same probleme with fit parameters error, but the function used to fit is not a polynom.
I have some data points and used another application to help me to find the function, that is PearsonIV with 6 parameters. This application gives me the coefficient values and I used them to set starting values of these parameters into ROOT.
This fitting function looks goof in Root, values of the parameters agrees with those given by the other application but … the error on these coefficient is huge : at least 10^4 bigger than the value of the coefficient.
How to explain that, and how to “configure” my macro to fit properly, with acceptable errors on coefficients?
thanks a lot,