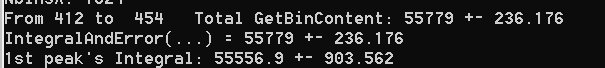Error calculation PROBLEM for Integral method in TF1 with comparison to either GetBinError() or IntegralAndError() in TH1

[spyhunter01]

Dear All,
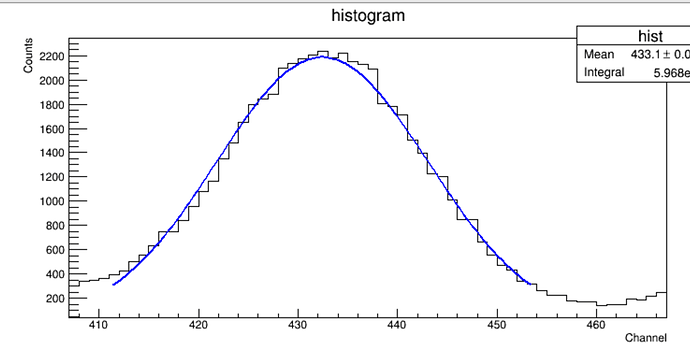
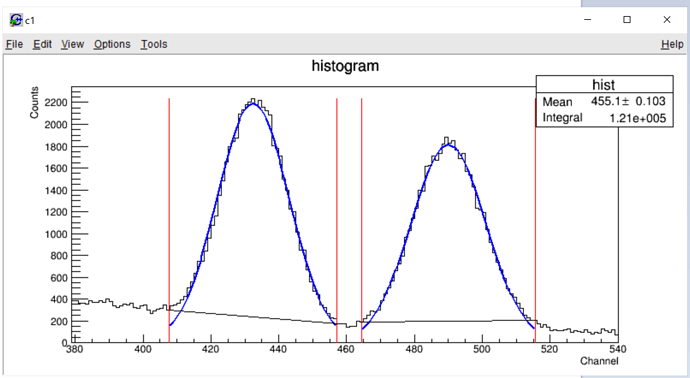
I had an histogram plotted, and then one Gaussian function fitted on that data.
By using both GetBinError() and IntegralAndError()methods, I got the same error for both in my histogram. That’s what I was expecting. Thus, everything look alright by that point.

Then, I fitted my Gaussian, and I used Integral() and IntegralError() methods to get my integral and its error. I was expecting, surely, lower counts due to the integral’s estimations from the function. However, the error turned out almost 4 times higher. FIRST OF ALL, is that what we should be expecting? Namely, is it OK? Otherwise, why did it become higher but not lower than the histogram’s error by following the same decrease pattern?

Just to give an idea, I put that bit of the code:
//////////////////////////////////////////////////////////// 1 way to get the error and integral from TH1 //////////////////////////
for (int i = LL; i < UL+1 ; i++ ){
TotalCounts += h1->GetBinContent(i);
TotalError += std::pow(h1->GetBinError(i), 2.);
}
TotalErrorUpdated= sqrt(TotalError);

cout <<“From " <<LL << " to " << UL <<” Total GetBinContent: " << TotalCounts <<" ± " << TotalErrorUpdated << endl;

//////////////////////////////////////////////////////////// Another way to get the error and integral from TH1 //////////

double myerror;
double myintegral = h1->IntegralAndError(LL, UL, myerror, “”); // “” … or … “width”
cout << "IntegralAndError(…) = " << myintegral << " ± " << myerror << endl;

///////////////////////////////////////////////////////////// 1 way to get the error and integral from TF1 //////////////////////////

double GrossArea1 = g1->Integral(xVmin, xVmax) ;// ConfidenceLimitCorrection;
double Error_GA1 = g1-> IntegralError(xVmin, xVmax , gaussParameters, MyConvarienceMatrix) ;
cout <<"1st peak’s " << "Integral: "<< GrossArea1 << " ± "<< Error_GA1 << endl;

/////////////////////////////////////////////////////////////////////////////////////////

[moneta]

Hi,
A difference could be in the interpretation of the value. TH1::IntegralAndError returns value in terms of bin contents. TF1::Integral and TF1::IntegralError returns the integral of the function, which contains then the histogram bin width. If you want the integral to represent number of events you need to divide integral and error by the bin width.
However in your case the bin width seems to be equal to 1.
I would need then the full running script including the histogram object, to reproduce and understand your problem
Best regards

Lorenzo

[spyhunter01]

Histogram bin width was set to 1. I was aware of dividing by the bin width if it wasn’t set to 1.
FindFittingValues.cpp (16.5 KB)

I am in the code testing stage, so I keep editing things once I clear the points I was working on. I want to make sure the code is doing what I meant to do.
Co60.txt (3.5 KB)

[moneta]

Hi,
Looking at the code, the problem seems to be the covariance matrix. You should get it from the fit.
I see also that you are using the fit error and fill just the diagonal terms. You should use the square of the errors for the diagonal and probably you should not neglect the correlations.
As example do:

auto r1 = h1->Fit(g1,"RS");
auto covMatrix = r1->GetCovarianceMatrix();
double Error_GA1  = g1->IntegralError(xVmin, xVmax , gaussParameters, covMatrix.GetMatrixArray()) ;

Lorenzo

[spyhunter01]

Hi Lorenzo,

This is what I got after changing what you said.

Now, errors look closer to each other. Most of the time, I am not sure what the method does. Then, I look into details from the definition. However, sometimes I might not get 100% from there, either.

The way I was using was taught to me by a friend long time ago, probably he didn’t know the details as well at that time.

When you said I should get the covariance matrix from the fit, wasn’t it doing it in that way! Since we retrieve error parameters from the fit, I thought it did. The standard deviation is 𝜎_𝑁=√(𝑣𝑎𝑟(𝑁) ), so the matrix elements should be square of 𝜎 to be the variance. I GOT IT. Probably, I should read this link to understand the purpose of using it.
You also said I shouldn’t neglect the correlations, but I saw the guy in the article was assuming the bin contents were independent from each other. I am not sure if you guys are talking about the same concept of correlation.

BTW, I change the line where I wrote "h1->Fit(g1,“R”); " instead I put auto r1 = h1->Fit(g1,“RS”); . I assumed it worked fine. Thanks.

[moneta]

@spyhunter01

You also said I shouldn’t neglect the correlations, but I saw the guy in the article was assuming the bin contents were independent from each other. I am not sure if you guys are talking about the same concept of correlation.

I was referring not to the correlations within bins, that are in general not present, but to the correlations between fit parameters which are present and they need to take into account when propagating errors from fit parameters to a derived quantity such as the function integral.
In general, it would also be better to determine the function normalisation (integral) directly from the fits. It can be done using the special functionality of summing normalized functions, when constructing the TF1 class representing signal plus background. See the tutorial ROOT: tutorials/fit/fitNormSum.C File Reference

Lorenzo