Hello,
I have a 3008 X 3008 data covariance matrix that’s nearly singular (eigenvalues span -1.e-15 -> 8.0; condition number ~2.e18). I’m trying a number of different ways to sidestep inverting the covariance matrix, one of which is doing an eigenvalue/vector decomposition and then transforming my data into a basis where the covariance matrix should be diagonal, and doing all my work in that basis. I notice that in this eigen decomposition of the covariance matrix, eigenvalues 0->999 are in a reasonable range (~0.1->8.0) but eigenvalues 1000->3008 are all tiny (-1.0e-15->1.0e-14). Is there something special about computing the eigenvalues after the first 1000 that is leading to this behavior? I realize that it’s possible that the rank of my covariance matrix is essentially equal to 1000, but I want to make sure that this is just a coincidence.
Thank you
P.S. In my earlier attempts to invert this covariance matrix, I’ve tried the normal tricks to force positive-definiteness by adding to the diagonal, etc. None of these worked, and Choleski decomposition still failed. 
. I’ve also tried fitting all my data using the SVD of the design matrix, as in the ROOT tutorial, still with no luck. Any broader suggestions here would be greatly appreciated.
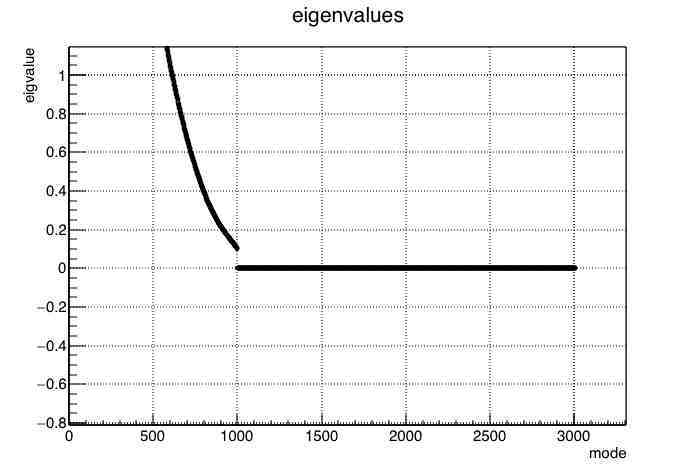
Just to follow up, the TMatrixDSymEigen class does compute different ranges of eigenvalues differently. In the attached plot of eigenvalues vs. mode, you can see this from the discontinuity at the 100th and 1000th eigenvalue.
I believe that this eigensystem solvers uses the LAPACK fortran package, which is used nearly everywhere (for example, I run into an identical problem if I try to use Mathematica).
There must be a good numerical reason for dividing the eigenvalues into these ranges, but am still wondering if there is some tolerance parameter, or separate ROOT linear algebra solver, to eliminate this behavior with the eigenvalues.
If you look in the code you will see that a tolerance number of 2^-52 = 2 10^-16 is used
as to be expected in double precision (64 bit) . Your eigen value range span is at least as
large.
Algorithms are based on EISPACK
I would have to refresh my algebra to be really sure, but I think when you diagonalize a rank r matrix, then you should expect to get only r eigenvalues that are not equal to zero.
Probably a better way to get the eigen values/vectors of the covariance matrix covM is
TDecompSVD svd(covM);
svd.SetTol(1.e-8); // set minimum eigenvalue through this ratio
svd.Decompose();
const TVectorD eigVal = svd.GetSig();
const TMatrixD eigVec = svd.GetV();
. I’ve also tried fitting all my data using the SVD of the design matrix, as in the ROOT tutorial, still with no luck. Any broader suggestions here would be greatly appreciated.
