Creating a normal distribution fit

[seley]

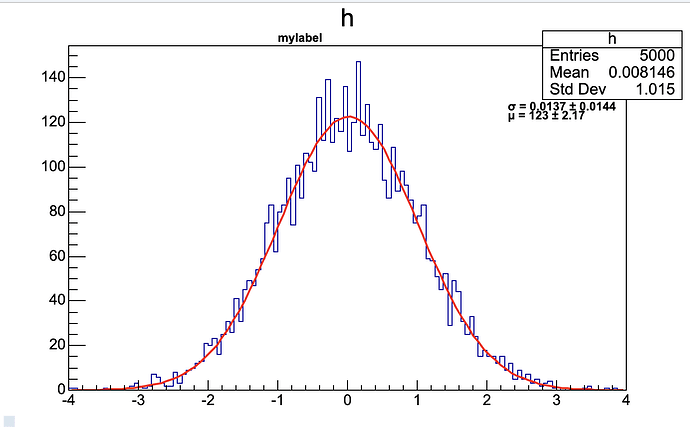
Hi,
I’m currently using pyroot to try to fit my histogram with a normal distribution and output both the mean and standard deviation.

    f = R.TFile(outfile, "UPDATE")
    c = R.TCanvas()
    # Get histogram pointer
    hist = DiffTrack_Truth_X.GetPtr()
    # Define a normal distribution manually based on the histogram's mean and standard deviation
    mean = hist.GetMean()
    std_dev = hist.GetStdDev()
    # Ensure std_dev is not zero to avoid division by zero
    if std_dev == 0:
        raise ValueError("Standard deviation is zero, cannot fit a normal distribution.")
    # Define the normal distribution function using the histogram's mean and std dev
    #mean =0 std_dev=1
    normal="1/([2]*sqrt(2*pi))*exp(-0.5*((x-[1])/[2])**2)"
    x_min=hist.GetXaxis().GetXmin()
    x_max=hist.GetXaxis().GetXmax()
    f1=R.TF1("normal",normal, x_min, x_max)
    # Draw the histogram
    hist.Draw()
    # Draw the normal distribution function on the same canvas
    f1.Draw("Same")
    # Add LaTeX labels
    lt = R.TLatex()
    lt.SetTextSize(0.03)
    # Label for additional text (you need to define `latexLabel`)
    lt.DrawLatexNDC(0.4, 0.91, latexLabel)
    # Format and display mean and standard deviation with errors (you might want to fit this first to get errors)
    lt.DrawLatexNDC(0.73, 0.73, f"#mu = {f1.GetParameter(0):.3g} #pm {f1.GetParError(0):.3g}")
    lt.DrawLatexNDC(0.73, 0.75, f"#sigma = {f1.GetParameter(1):.3g} #pm {f1.GetParError(1):.3g}")
    # Update the canvas and save
    c.Update()
    c.Write()
    f.Close()

However it is not drawing the fit, where am I going wrong?

Please read tips for efficient and successful posting and posting code

Please fill also the fields below. Note that root -b -q will tell you this info, and starting from 6.28/06 upwards, you can call .forum bug from the ROOT prompt to pre-populate a topic.

ROOT Version: Not Provided
Platform: Not Provided
Compiler: Not Provided

---

[Danilo]

Hi,

I simplified a bit the code to show how this can work, hopefully this is of help:

import ROOT as R

# Get histogram pointer
# hist = DiffTrack_Truth_X.GetPtr()
hist = R.TH1D("h", "h", 128, -4, 4)
hist.FillRandom("gaus")

# Define a normal distribution manually based on the histogram's mean and standard deviation
std_dev = hist.GetStdDev()
# Ensure std_dev is not zero to avoid division by zero
if std_dev == 0:
    raise ValueError("Standard deviation is zero, cannot fit a normal distribution.")

hist.Fit("gaus")
f1 = hist.GetFunction("gaus")

x_min=hist.GetXaxis().GetXmin()
x_max=hist.GetXaxis().GetXmax()

# Draw the histogram
hist.Draw()

# Add LaTeX labels
lt = R.TLatex()
lt.SetTextSize(0.03)
# Label for additional text (you need to define `latexLabel`)
latexLabel = "mylabel"
lt.DrawLatexNDC(0.4, 0.91, latexLabel)
# Format and display mean and standard deviation with errors (you might want to fit this first to get errors)
lt.DrawLatexNDC(0.73, 0.73, f"#mu = {f1.GetParameter(0):.3g} #pm {f1.GetParError(0):.3g}")
lt.DrawLatexNDC(0.73, 0.75, f"#sigma = {f1.GetParameter(1):.3g} #pm {f1.GetParError(1):.3g}")

Result:

Cheers,
D