Hi. I’m trying to fit some data to a function. The function I want to fit is the convolution of three exponentials and a gaussian. The code I’ve writte is this:
eventcon[4] = new TCanvas ("Evento","Evento",1800,1200);
TF1 *fexp1 = new TF1("fexp1","[0]*exp(-(x-[7])/[1]) + [2]*exp(-(x-[7])/[3]) + [4]*exp(-(x-[7])/[5]) +[6]*exp(-0.5*((x-[7])/[8])*((x-[7])/[8]))",0,4000);
fexp1->SetLineColor(kRed);
fexp1->FixParameter(1,7); // Singlet lifetime
fexp1->FixParameter(7,665); // Time t0
fexp1->SetParLimits(0,1 ,15); //Singlet amplitude
fexp1->SetParLimits(2,1,15); // Medium amplitude
fexp1->SetParLimits(3,10,300); // Medium lifetime
fexp1->SetParLimits(4,1,15); //Triplet amplitud
fexp1->SetParLimits(5,1400 ,1700); // Triplet lifetime
fexp1->SetParLimits(6,1,15); //Gaussian amplitude
fexp1->SetParLimits(8,17,23); //Sigma
gPad->SetLogy();
event[4]->Draw("E");
event[4]->Draw("SAME Lhist");
event[4]->Fit(fexp1,"R");
fexp1->Draw("SAME");
event[4]->SetAxisRange(0.1,150,"Y");
eventcon[4]->Print("fitWaveform.pdf");
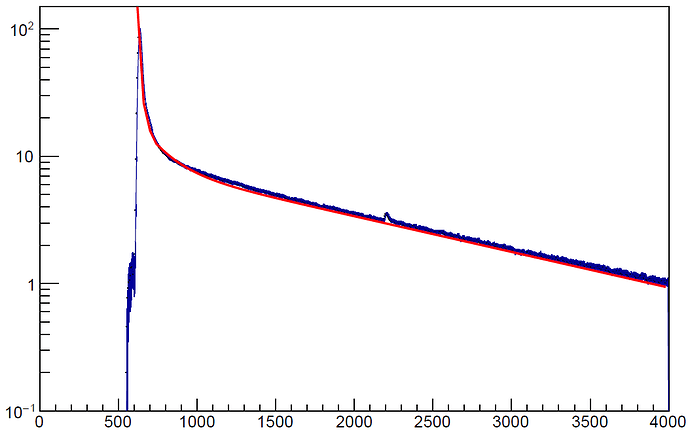
This is the result I obtain, and I don’t know how to improve it because I’m new in Root:
It is a regular/good fit after de maximum, but I need to fit the part at the left part of the maximum too.