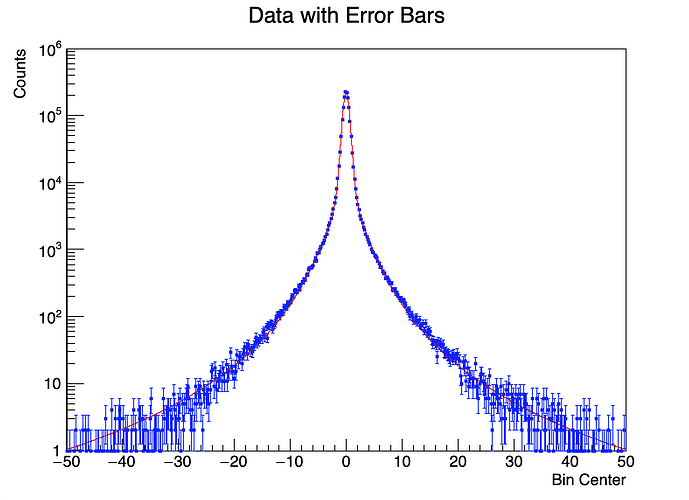
Hi,
Complete newbie here.
I am following a paper here, that describes a way to fit multiple scattering distributions, using a Student’s t distribution, convoluted with a Gauss. The formulae of interest are 3.1 and 3.2. To this end, I have few, punctual problems:
-
At the moment, I manage to fit the convolution of a Gauss and Student’s t, but probably the fit can be improved, since the chi2ndof is ~8. Changing the initial guesses does not help much (I even tried putting the values from the minimization as initial parameters)… Anything else I can do to improve the fit? Is my understanding wrong (i.e. that one takes the results of the minimization and uses them for an improved initial guess)?
(Also, at the same time, if I include the error in the x, the fit does not work anymore. For now, I replace those with zeroes.) -
Moving further to reproducing formula 3.2, which convolutes yet again the previous convolution of Gauss and Student’s t with another Student’s t, I am kind of stuck (basically no idea what I’m doing…)
I tried following some tutorials and answers I found on the forum to write the integral, but I did not manage (you can see my attempt is commented, both the definition of the function and the fit).
I also don’t understand if the parameters should be different from the first Student’s t distribution or not…
Moreover, with these initial parameters, I get:Warning in <ROOT::Math::ROOT::Math::GausIntegrator>: Failed to reach the desired tolerance ; maxtol = 1e-09
What can I do in this case?
Thank you very much for your help!
PS: I am aware of some code from one of the authors, asked on the forum ( … fit-convolution-of-two-functions-doesnt-converge/16507), however it does not help me much… and probably a few things changed since 2013 ![]()
My data can be found here:
scatt_data.zip (2.8 KB)
The code that I have so far can be found below.
#include <fstream>
#include <sstream>
#include <string>
#include <vector>
#include <TGraphErrors.h>
#include <TCanvas.h>
#include <TAxis.h>
#include <TF1.h>
#include <TCanvas.h>
#include <TMath.h>
#include <Math/Functor.h>
#include <iostream>
double fitFunction(double *x, double *par) {
double theta = x[0];
double N = par[0];
double a = par[1];
double mu = par[2];
double sigma_g = par[3];
double sigma = par[4];
double tail_parameter = par[5];
double gaussian_part = (1 - a) * TMath::Gaus(theta, mu, sigma_g, kTRUE);
double z = (theta - mu) / sigma;
double t_part = a * TMath::Student(z, tail_parameter) / sigma;
return N * (gaussian_part + t_part);
}
// double convolutionIntegral(double *x, double *par) {
// double theta = x[0];
// ROOT::Math::Functor1D convolutionFunc([&](double tau) {
// double tempX[1] = {theta - tau};
// return fitFunction(tempX, par);
// });
// ROOT::Math::Integrator integrator(convolutionFunc);
// double lowerLimit = -10; // no clue?!
// double upperLimit = 10;
// double integral = integrator.Integral(lowerLimit, upperLimit);
// return integral;
// }
void readcsv() {
std::string filePath = "scatt_data.csv";
std::ifstream inFile(filePath);
std::string line;
std::getline(inFile, line); // skip the header
double bin_center, count, errorx, errory;
std::vector<double> bin_centers, counts, errorsx, errorsy;
while (std::getline(inFile, line)) {
std::istringstream iss(line);
std::string value;
std::getline(iss, value, ',');
bin_center = std::stod(value);
std::getline(iss, value, ',');
count = std::stod(value);
std::getline(iss, value, ',');
errorx = std::stod(value);
std::getline(iss, value, ',');
errory = std::stod(value);
bin_centers.push_back(bin_center);
counts.push_back(count);
errorsx.push_back(errorx);
errorsy.push_back(errory);
}
int nPoints = bin_centers.size();
double *x = bin_centers.data();
double *y = counts.data();
double *ex = new double[nPoints];
std::fill_n(ex, nPoints, 0);
double *ey = errorsy.data();
// double *ex = errorsx.data(); // fit fails if I use this ... todo
TGraphErrors *graph = new TGraphErrors(nPoints, x, y, ex, ey);
graph->SetMarkerStyle(21);
graph->SetMarkerColor(kBlue);
graph->SetLineColor(kBlue);
TF1 *fitFunc = new TF1("fitFunc", fitFunction, -50, 50, 6);
fitFunc->SetParameters(300000, 0.05, 0, 0.6, 3, 3); // Initial guesses for N, a, mu, sigma_g, sigma, tail
graph->Fit(fitFunc, "F", "", -50, 50);
fitFunc = graph->GetFunction("fitFunc");
fitFunc->GetNDF();
fitFunc->GetChisquare();
fitFunc->GetProb();
std::cout << "Chi-squared: " << fitFunc->GetChisquare() << std::endl;
std::cout << "NDF: " << fitFunc->GetNDF() << std::endl;
std::cout << "Probability: " << fitFunc->GetProb() << std::endl;
std::cout << "Parameters:" << std::endl;
for (int i = 0; i < fitFunc->GetNpar(); ++i) {
std::cout << "Param " << i << ": " << fitFunc->GetParameter(i) << " +/- " << fitFunc->GetParError(i) << std::endl;}
// TF1 *convolutionFitFunc = new TF1("convolutionFitFunc", convolutionIntegral, -50, 50, 6);
// convolutionFitFunc->SetParameters(10000, 0.5, 0, 3, 3, 2); // N, a, mu, sigma_g, sigma, tail
// graph->Fit(convolutionFitFunc, "F", "", -50, 50);
// TF1 *fitResult = graph->GetFunction("convolutionFitFunc");
// std::cout << "Chi-squared conv: " << fitResult->GetChisquare() << std::endl;
// std::cout << "NDF conv: " << fitResult->GetNDF() << std::endl;
// std::cout << "Probability conv: " << fitResult->GetProb() << std::endl;
// std::cout << "Parameters conv:" << std::endl;
// for (int i = 0; i < fitResult->GetNpar(); ++i) {
// std::cout << "Param conv " << i << ": " << fitResult->GetParameter(i) << " +/- " << fitResult->GetParError(i) << std::endl;
// }
TFile *file = new TFile("scattering_data.root", "RECREATE"); // need later
graph->Write("scattering");
file->Close();
delete file;
TCanvas *c1 = new TCanvas("c1", "Data with Error Bars", 800, 600);
gPad->SetLogy();
graph->SetTitle("Data with Error Bars;Bin Center;Counts");
graph->Draw("AP");
graph->GetXaxis()->SetLimits(-50, 50);
graph->SetMinimum(1);
graph->SetMaximum(1000000);
c1->Update();
}
int read_py() {
readcsv();
return 0;
}
ROOT Version: 6.24/06
Platform: linuxx8664 (WSL2 on Windows)
Compiler: gcc