Dear rooters,
I am trying to fit a TH1 (which is the ratio of two histoograms) in a control region in order to extrapolate a correction factor to some yields in a signal region.
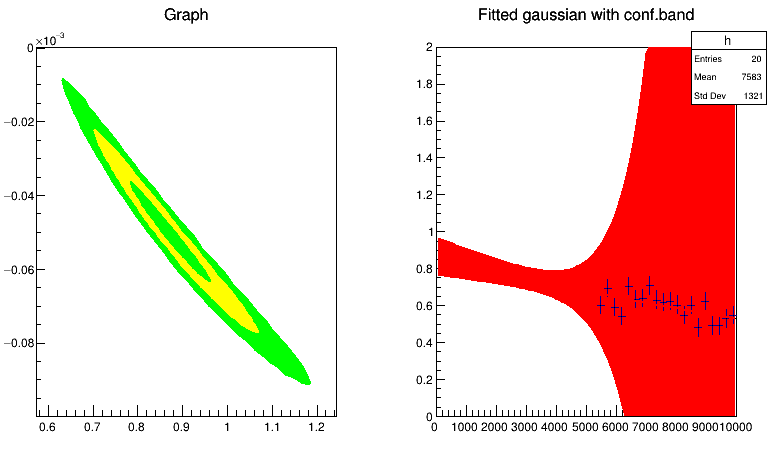
I am fitting the ratio of the histograms with an exponenential function. In order to understand the impact of the error on the parameters on the fit function, I am plotting the 68% confidence level on the function using the GetConfidenceInterval function of the TFitter class.
The code is basically readapted from one of the tutorials.
#include "TGraphErrors.h"
#include "TGraph2DErrors.h"
#include "TCanvas.h"
#include "TF2.h"
#include "TH1.h"
#include "TVirtualFitter.h"
#include "TRandom.h"
#include "TFitResultPtr.h"
#include "TMinuit.h"
void ConfidenceIntervals()
{
//gROOT->SetBatch(1);
//TVirtualFitter::SetDefaultFitter("Minuit");
TRandom* random = new TRandom();
TCanvas *myc = new TCanvas("myc",
"Confidence intervals on the fitted function",1200, 500);
myc->Divide(3,1);
TF1 *f = new TF1("fexp", "[0]*exp(x*[1])", 5300, 10000);
//TF1 *f = new TF1("fexp", "[0]+[1]*x", 5300, 10000); //This looks reasonable
f->SetParameters(0.77, -0.00004);
////2. A histogram
myc->cd(2);
//Create, fill and fit a histogram
Int_t nh=5000;
TH1D *h = new TH1D("h",
"Fitted gaussian with conf.band", 43, 0, 10000);
h->GetYaxis()->SetRangeUser(0., 2.);
//h->FillRandom("fgaus", nh);
for (int i=1; i<44; ++i){
double value = f->Eval(h->GetBinCenter(i));
value = value * random->Gaus(1, 0.10);
if (h->GetBinCenter(i)>5300){
h->SetBinContent(i, value);
h->SetBinError(i,0.05);
}
}
f->SetParameters(1., 0);
f->SetLineWidth(2);
h->Fit(f, "EV");
h->Draw();
//Create a histogram to hold the confidence intervals
TH1D *hint = new TH1D("hint",
"Fitted exponential with conf.band", 100, 0, 10000);
(TVirtualFitter::GetFitter())->GetConfidenceIntervals(hint, 0.68);
//Now the "hint" histogram has the fitted function values as the
//bin contents and the confidence intervals as bin errors
hint->SetStats(kFALSE);
hint->SetFillColor(2);
hint->Draw("e3 same");
h->Draw("same");
myc->cd(1);
gMinuit->SetErrorDef(9);
TGraph *graph3 =(TGraph*) gMinuit->Contour(80, 0,1);
graph3->SetFillColor(kGreen);
graph3->Draw("alf");
gMinuit->SetErrorDef(4);
TGraph *graph2 =(TGraph*) gMinuit->Contour(80, 0,1);
graph2->SetFillColor(kYellow);
graph2->Draw("lf, same");
gMinuit->SetErrorDef(1);
TGraph *graph =(TGraph*) gMinuit->Contour(80, 0,1);
graph->SetMarkerColor(kGreen);
graph->SetFillColor(kGreen);
graph->Draw("lf,same");
//graph->Draw("alf,same");
return;
}
As you see from the following plot, the confidence band just explodes at high x. And what is also surprising is that it explodes where the points are located.
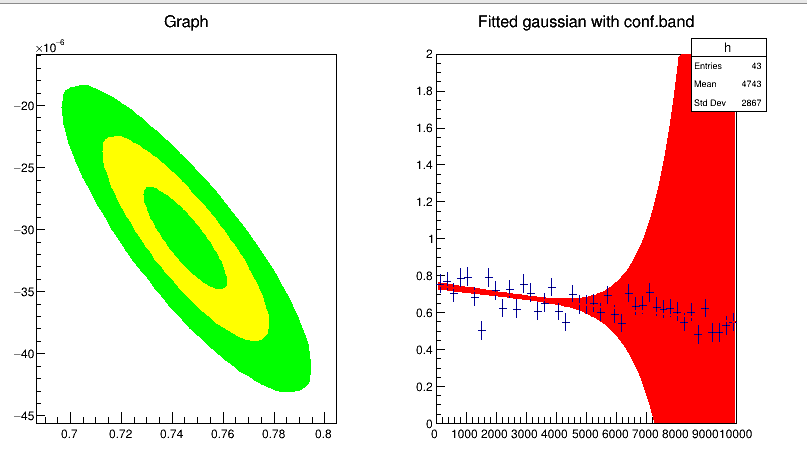
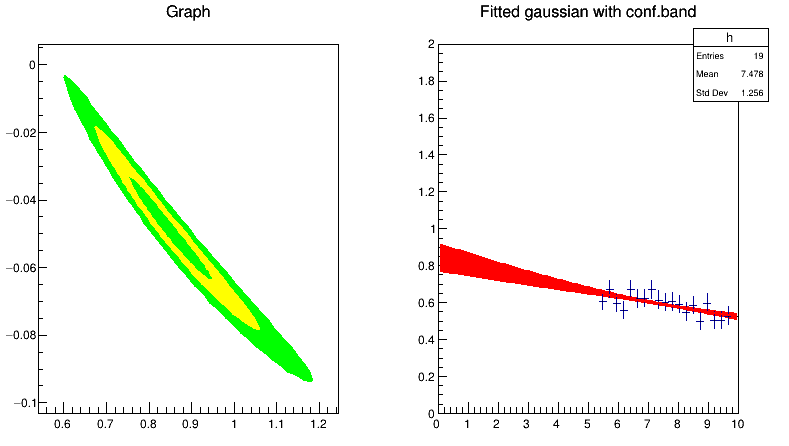
At first I thought it was only a problem of a non so parabolic chi2 around the minimum (the plot on the left). But adding more points, and with a more parabolic chi2, the feature remains.
I know that the evaluation of the error band is done using the linear approximation in the error propagation formula. So is what I see only a problem arising from the fact that the function is not linear in the parameters? If I use a linear model, than the error is well behaved, but I would like to fully understand why this is happening with the exponential and why in this strange way.
Thanks a lot for any help
_ROOT Version: 6.14
Platform: Not Provided
Compiler: Not Provided