Dear ROOT experts,
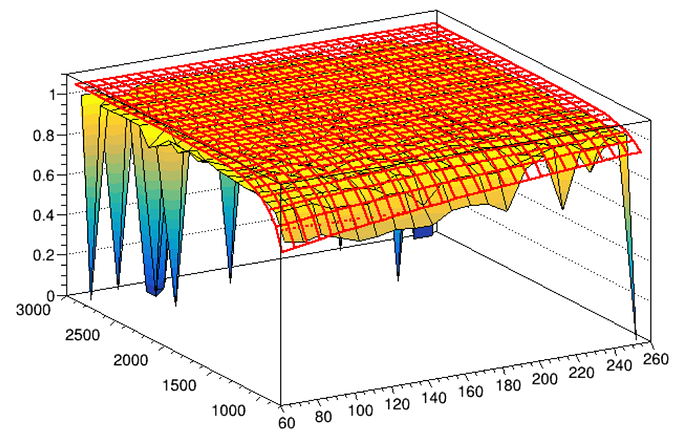
I am doing an analysis in which I create two-dimensional trigger efficiencies and store both the TEfficiency and TH2F from TEfficiency::CreateHistogram() in a ROOT file. I can successfully fit the histogram with a parametric TF2, but now I’d like to be able to evaluate the function at a given point and recover f(X,Y;p0,p1,p2,...) = value +/- error. The fit itself looks like this:
I could write a method which computes the function uncertainty from the covariance matrix, but while researching whether this was implemented already in vanilla ROOT (instead of having to use RooFit), I came across this old forum post, which indicated that the FitResult::GetConfidenceIntervals() method could help. However, for a 2D function I’m somewhat unsure as to how one should interpret the results of this method. I’ve attached a code snippet and give its output below to help illustrate my confusion.
void evalFuncUncertainty() {
// Open file, get TEfficiency, create TH2 which we'll fit
TFile* f = new TFile("THtrigger2D_HT750_18.root","READ");
TEfficiency* eff = (TEfficiency*)f->Get("Pretag");
TH2F* h = (TH2F*)eff->CreateHistogram();
// Create function, set decent starting parameters
TF2* func = new TF2("eff_func","1-[0]/10*exp([1]*y/1000)*exp([2]*x/200)",60,260,800,2600);
func->SetParameter(0,550);
func->SetParameter(1,-5);
func->SetParameter(2,-1);
// Fit function to histogram, get TFitResultPtr
TFitResultPtr r = (TFitResultPtr)h->Fit(func,"SER");
// Evaluate fit results
printf("The fit uses %d X points and %d Y points\n",func->GetNpx(),func->GetNpy());
printf("The fit uses %d fit points\n",func->GetNumberFitPoints());
// Now, check that everything makes sense with the covariance matrix
printf("The covariance matrix is given by:\n");
r->GetCovarianceMatrix().Print();
// Check that covariance matrix is as expected
float par0Cov = r->CovMatrix(0,0);
float SqrtPar0Cov = TMath::Sqrt(par0Cov);
float par0err = func->GetParError(0);
printf("Covariance & uncertainty checks:\n\tCov[p0,p0] = %f\n\tSqrt(Cov[p0,p0]) = %f\n\tp0 error = %f\n\n",par0Cov,SqrtPar0Cov,par0err);
// Now try to get uncertainty at a given point straight from the fit
std::vector<double> CL = r->GetConfidenceIntervals(0.683,true);
printf("The confidence levels were evaluated at %u points\n", CL.size());
}
The output is as follows:
Processing evalFuncUncertainty.C...
Info in <TCanvas::MakeDefCanvas>: created default TCanvas with name c1
FCN=0.752307 FROM MINOS STATUS=SUCCESSFUL 460 CALLS 1789 TOTAL
EDM=6.55355e-07 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 5.29474e+02 8.94639e+03 -2.10905e-02 -1.85028e-05
2 p1 -5.85658e+00 1.90164e+01 5.90370e-02 5.97904e-05
3 p2 -1.03439e+00 3.59615e+00 3.59615e+00 -4.28703e-07
The fit uses 30 X points and 30 Y points
The fit uses 357 fit points
The covariance matrix is given by:
3x3 matrix is as follows
| 0 | 1 | 2 |
--------------------------------------------
0 | 8.004e+07 -1.683e+05 -1206
1 | -1.683e+05 361.6 -6.497
2 | -1206 -6.497 12.93
Covariance & uncertainty checks:
Cov[p0,p0] = 80037840.000000
Sqrt(Cov[p0,p0]) = 8946.386719
p0 error = 8946.386719
The confidence levels were evaluated at 357 points
The 2D fit is using its default 30x30 points in the fit, but TF2::GetNumberFitPoints() returns only 357 points. These 357 points are clearly the ones at which the confidence levels are being evaluated, but several things are unclear to me:
- How would one determine to which (x,y) points in the TH2 the points whose confidence intervals were evaluated in the fitted function correspond?
- Why are all 30x30=900 points in the fit not evaluated? My thought was perhaps empty bins in the histogram are not evaluated, but there were not enough empty bins in the histogram to explain the 543 non-evaluated points.
- The 2D
TEfficiencyhas asymmetric errors. Are these errors propagated to the TH2 created viaTEfficiency::CreateHistogram()and should I therefore callFitResult::GetConfidenceIntervals()with the argumentnorm=false?
Apologies for the long post, but I hope my questions are clear. Thank you very much in advance for any insights and explanations.
ROOT Version: 6.24/04