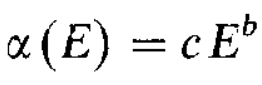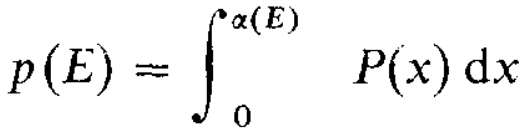Hello rooters,
I’m trying to define the following functions:
where P(x) is a chi-square distribution with one degree of freedom.
What I’ve done so far is the following:
TF1 *f_Porter_Thomas = new TF1("f_Porter_Thomas", "ROOT::Math::chisquared_pdf(x,1,0)",0,10);
TF1 *f_alpha = new TF1("f_alpha", "[0]*pow(x,[1])" , E_low, E_high);
and it’s nothing complicated. I’m having hard time, though, defining a TF1 the would include TF1::Integral().
So for example this doesn’t work:
TF1 *f_p = new TF1("f_p" , "f_Porter_Thomas->Integral(0, 10)", E_low, E_high);
What I get is:
input_line_321:2:105: error: member reference type 'double' is not a pointer
Double_t TFormula____id9601315710509570316(Double_t *x){ return (ROOT::Math::chisquared_pdf(x[0],1,0))->Integral(0,10) ; }
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ^
input_line_322:2:105: error: member reference type 'double' is not a pointer
Double_t TFormula____id9601315710509570316(Double_t *x){ return (ROOT::Math::chisquared_pdf(x[0],1,0))->Integral(0,10) ; }
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ^
Error in <prepareMethod>: Can't compile function TFormula____id9601315710509570316 prototype with arguments Double_t*
Eventually I would like to be able to define the TF1 like so:
TF1 *f_p = new TF1("f_p" , "f_Porter_Thomas->Integral(0, <f_alpha(x)>)", E_low, E_high);
Any idea on how to do that?
Thanks in advance!