Building Neyman-Pearson test in 2D-space having only data for null- and alternative hypothesis

ROOT
1

Disclaimer

I know that it is not the best place to ask my question. But I know there are a lot of competent people who could help me here.

Problem

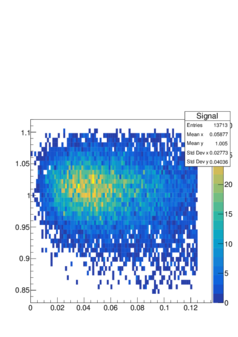
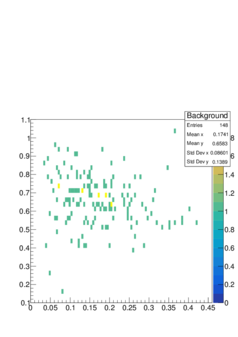
Suppose we have some statistical data which is represented as 2D histogram.

The problem can be formulated as the following:

Given a significance level a and two sample sets which is known that one of them is a signal and other is a background (see figures) determine critical region S that gives largest power 1-ß with respect to the alternative hypothesis. In other words, it is needed to choose a region in order to reject as much background as possible accepting signal with efficiency a.

The problem is more about some computational algorithm rather than some theoretical approach. Though everything is connected. Also see here for more details.

Any ideas how it can be done.
EtotvsPtotsig2EtotvsPtotbg2

2

Hi,

If you have data for H0 and H1 you can use a supervised method to perform your test.
See in ROOT the TMVA package (https://root.cern.ch/tmva ) which provide several algorithms for doing this.

Lorenzo

3

This topic was automatically closed 14 days after the last reply. New replies are no longer allowed.