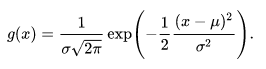ROOT Version: 6.14.00
Platform: Ubuntu 20.04 LTS
Compiler: gcc
Dear experts,
I would like to kindly ask for your help.
As a distribution, I want to add a gaussian pdf generated from the given mean(Ea) and sigma. N = sum of na.
From this table,
I want to calculate the total Probability Distribution given using :
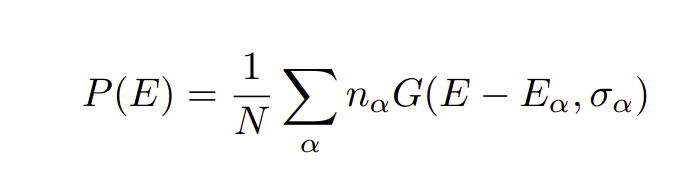
And find the E distribution from above and add it here:
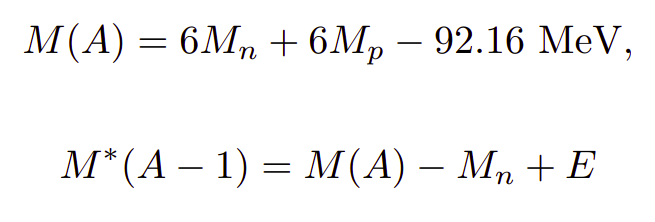
where, M(A) , Mn, Mp are constant values.
Here is my attempted code:
#include <string>
#include <iostream>
#include <fstream>
#include <cmath>
#include <vector>
//#include "TH1D.h"
using namespace std;
//Calculate Probability Distribution Function
double norm_pdf(double x, double mu, double sigma, double na)
{
return na* exp( -((x - mu)*(x-mu))/(2.0*sigma*sigma) );
}
void generateNormPdf(double mu[], double sigma[], double na[], vector<double>& x, vector<double>& density)
{
double N = 22.0; // Total number of neutrons (na)
int nev = x.size(); // Number of points to generate between min_range and max_range
double min_range = 0.0;
for (int i = 0; i<7; i++){ // 7 is size of sample
for (int j = 0; j<nev; j++)
{
x[j] = (mu[i]*2.0 - min_range)/(nev-1) * j;
density[j] = (1.0/N)*norm_pdf(x[j], mu[i], sigma[i], na[i]);
}
}
}
int main()
{
int nev = 100; // Number of samples/events
// PDF
vector<double> x(nev);
vector<double> density(nev);
double mu[] = {62.0,40.0,35.0,18.0,13.15,11.45,5.56}; // Mean
double sigma[] = {6.25,3.75,3.75,1.25,1.0,0.75,0.75}; // Standard Deviation
double na[] = {2.0,4.0,2.0,2.6,2.0,4.0,2.0}; // # of nucleons
generateNormPdf(mu, sigma, na, x, density);
}
The final value I want is M*(A-1) as distribution (i.e not a constant value).
It would be of great help.
Thanks in advance.